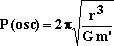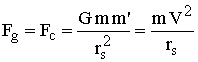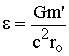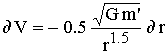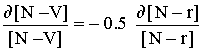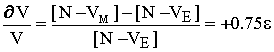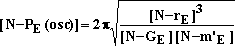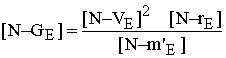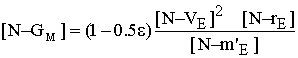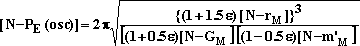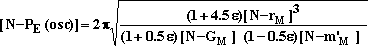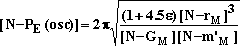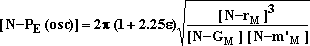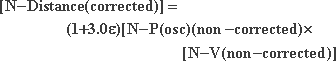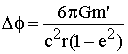A Detailed Classical Description of the
Advance of the Perihelion of Mercury.
P. Marmet, Physics
Department, University of Ottawa, Ottawa, Canada K1N 6N5
( Last checked 2018/01/15 - The estate of Paul Marmet
)
<><><><><><><><><><><><>
Abstract.
Using
Einstein's general relativity, it is generally believed that space
and time distortions are absolutely required to explain the
advance of the perihelion of Mercury. This is untrue. The advance
of the perihelion of Mercury was first calculated in 1898 by Paul
Gerber (1A). We show here that this phenomenon can be fully
explained using Newton's physics and mass-energy conservation,
without any relativity principle. Without having to introduce any
new physics, we arrive to the same equation as predicted by
Einstein. Therefore, the relativity principles are useless.
1-
Introduction.
A
preliminary classical demonstration of the advance of the
perihelion of Mercury has been given previously in the book: Einstein’s Theory of
Relativity versus Classical Mechanics, (chapters 5 and 6),
[1],without using any of Einstein's postulates. That
demonstration uses mathematical relationships, which are based
on classical mechanics and mass-energy conservation. We explain
now in detail, all the physical mechanisms involved in the
calculation of the advance of the perihelion of Mercury. Using
only classical mechanics, we obtain the same equation as
predicted by Einstein’s General Relativity, without using any of
the relativity principles. We have seen [1]
that the advance of the perihelion is due to gravitational
potential and kinetic energy, which modify the standard meter
and the clock rate on Mercury. The physical change of length and
the change of clock rate were demonstrated previously [1] . The only difference between the
usual Newton’s physics and the results presented here is that,
contrarily to Einstein, we fully take into account the principle
of mass-energy conservation. This paper shows how to use the
units existing on Mercury to derive the correct shape of the
precessing elliptical orbit around the sun.
2-
Orbital Motion.
An
ellipse with a small eccentricity is identical to a circular
orbit, in which the center of the circle has been slightly
shifted. This can be seen more easily when we examine in detail
the transformations of shapes from a circle to an ellipse. This
geometrical transformation is demonstrated in Appendix 1. However, when a circle is
slightly perturbed to become an ellipse, the change of shape is
usually described by the gradual transformation from a circle to
the familiar elongated characteristic shape of an ellipse. In
the case of the elliptical shape of an orbit around the sun,
since the eccentricity is small, this is equivalent to a circle
with a shifted center, because in fact, when adding a small
eccentricity, the first mathematical term of the series
expansion of an ellipse appears as a shift of the central
circular field of forces. It is only the second term of
the series expansion of an ellipse, which flattens the orbit
into the well-known elongated shape (see Appendix1).
This description is useful for a better understanding of the
physics discussed here.
Let us
consider a mass m orbiting the sun. Newton’s laws show that, due
to the centrifugal force, when the orbiting velocity is such
that the radius of curvature of the orbiting mass is compatible
with distance of a circular orbit around the sun, that radius of
curvature is stable. Such a circular orbit is illustrated
around the shaded area on figure 1. In that case, the moving
mass is always at the same constant distance ro from
the sun.
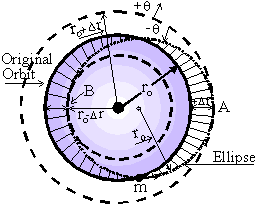
Figure 1
Consequently, in a circular orbit, the mass is continuously
subjected to a constant gravitational force, which is always
exactly compensated by an equal constant centrifugal force
everywhere on the orbit. The centrifugal force F(centri) and the
gravitational force F(grav) are exactly equal and opposite, so
that their sum is everywhere zero at the distance ro
from the sun. We have:
 |
1 |
In this
paper, only a single plane of the orbits needs to be
considered.
Let us
consider that at the distance ro from the sun, the
curved trajectory represents a curved axis of coordinates (the
curved horizontal axis on figure 2) along the circular trajectory
around the sun. Planet Mercury travels at a constant velocity V
along that curved axis. At radii r+Dr
and r-Dr, (dashed circles on figure 1),
the corresponding (dashed) parallel lines to the ro
axis are drawn on figure 2. Of course, there exists no force
F accelerating the mass along this tangential direction, since the
centrifugal force compensates for the gravitational force at ro.
This axis is perpendicular to a radial r-axis (drawn vertically on
figure 2).
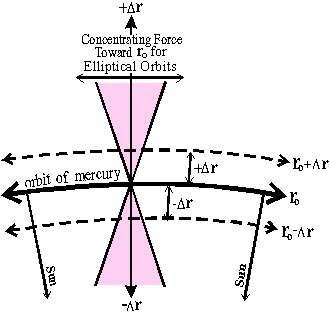
Figure 2
Since we
have seen in equation 1 that the two forces cancel out at a
distance ro, there remains no net force Fr,
in the radial direction, as long as the distance of the mass from
the sun remains ro.
If, at
one point on the orbit, the mass is deflected toward an outer
direction (illustrated at "m" on figure 1), its distance r from
the sun increases. However, its velocity will then gradually
decrease because of its increasing gravitational potential in the
new direction further away from the Sun. Therefore, the slower
particle will gradually have a "radius of curvature" (around the
aphelion in A, on figure 1) smaller than its distance (radius r+DR) from the Sun. This will then make the
mass fall back to a closer distance to the Sun. Then, when
approaching the perihelion B, inside the initial orbit ro, the velocity will then increase so that the radius of
curvature will now be larger than its distance from the Sun. This
phenomenon is repeated periodically at every rotation around the
sun.
This
qualitative description shows that in such an elliptical motion,
the mass oscillates (along the radial r-axis) from one side to the
other of the average radius ro,
as shown in dotted (not dashed) line on figure 1. Since the mass
oscillates on each side of the average radius ro, there must exists a net force, always pulling it in
the opposite direction, always toward ro. Let us calculate this force.
3 -
Constant Curvature of an Ellipse with a Small Eccentricity.
We can
see in Appendix I, a geometrical
demonstration showing that an ellipse with a small eccentricity
(first order) is identical to a circle in which the center has
been shifted. Therefore such an ellipse is a circle with a
displaced center (first order). Let us demonstrate now, that the
laws of physics also lead to a constant radius of curvature R
when a mass travels on an elliptical orbit (with a small
eccentricity). This means that the forces acting on the mass
orbiting on an ellipse, and the velocity must be compatible with
the constant (radius of) curvature R of the ellipse.
Let us
define the "radius of curvature" at one point on the ellipse
equal to R, while the distance from the sun is r. Therefore, R
is the distance from a point on the ellipse to the center of the
ellipse (point "C" on figure 7). Since an ellipse with a
small eccentricity is a circle with a radius R, the centrifugal
force must always lead to a constant radius of curvature R. We
have:
 |
2 |
The
radius of curvature R must remain constant even when the distance
r from the sun increases by ¶r.
Equation 2 gives:
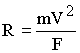 |
3 |
Since we
have an ellipse, the distance r from the Sun is a variable so that
the gravitational force F changes. Furthermore, the velocity V on
the orbit changes at the same time. Let us calculate an assumed
variation of the radius of curvature R (if any) as a function of
the gravitational force F and the velocity V of the orbiting mass.
The derivative of equation 3 is:
 |
4 |
This is
equivalent to:
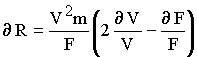 |
5 |
The
gravitational force F is equal to:
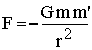 |
6 |
Its
derivative is:
 |
7 |
From
equations 6 and 7 we find:
 |
8 |
Let us
substitute 8 in 5, we find:
 |
9 |
Since the
velocity of the orbiting mass changes when changing its distance
from the Sun, let us apply the principle of energy conservation.
When r is changing, the variation of potential energy is equal
(minus) to the variation of kinetic energy. We have:
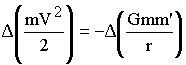 |
10 |
This
gives:
 |
11 |
or
 |
12 |
It is
well known in classical mechanics, that in a orbital motion around
a central field, the kinetic energy of an orbiting mass is always
(minus) half of the potential energy. Since this is well
known, this will not be repeated here. This can be written:
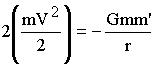 |
13 |
This
gives:
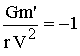 |
14 |
Substituting 14 in 12 gives:
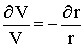 |
15 |
Equation
15 in 9 gives:
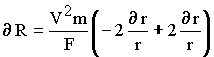 |
16 |
Equation
16 can also be written:
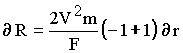 which is which is  |
17 |
Equation
17 shows that a change dr of distance
r from the Sun (in the neighborhood of ro), does not
change the radius of curvature R on any point on the elliptical
orbit. Since in equation 17 dR equals zero, this means that
in equation 5, the relative change of velocity dV/V just cancels out the effect due to
the change of gravitational force dF/F.
Therefore the elliptical orbit maintains everywhere the constant
curvature R, even if the distance from the Sun is variable. This
agrees with a circle with a displaced center as illustrated on
figure 1 (also in Appendix I).
4
-
Spring Constant
On
figure 1 and 2, we see a larger circular orbit at (ro+Dr) and a smaller circular orbit at (ro-Dr) illustrated by dashed lines, while
the elliptical orbit of Mercury is illustrated on figure 1 using
a dotted line. We can see (especially on figure 2), that those
circular trajectories at ro+Dr
(and ro-Dr) are parallel
to ro (at A and B). When the mass is located
in A, we see (figure 1) that the elliptical orbit does not
remain at a constant distance from the original circular orbit
(solid line). In order to remain at a constant distance, the
particle (on the elliptical orbit) would have to continue along
the dashed circular orbit having a radius ro+Dr. Therefore, with respect to this
circular orbit, there is a force on the elliptical orbit,
bringing the mass back toward the radius ro, when the
particle is A.
Similarly, when the elliptical orbit passes at the perihelion,
at point B, inside the initial orbit ro, there must
be a force pushing the mass back externally, toward the initial
radius ro. That force (pushing the mass back toward ro),
that exists for the elliptical orbit does not appear for the
circular orbit at ro-Dr.
Let us calculate that force (always pushing the particle back to
the radius ro).
It is
clear that the force pushing the particle back to the radius ro
at a distance ro±Dr, is
equal to the difference of force between the circular orbit and
the elliptical orbit passing by A or B. Both the elliptical and
the circular orbits pass through a common point at A, (where of
course the gravitational force is the same). Keeping
everything else (i.e. energy, velocity and potential) constant,
let us calculate the change of force necessary at A, so that the
radius of curvature of the mass in the elliptical orbit become
equal to the radius of curvature of the circular orbit. This is
the force we are looking for in order to make the two orbits
parallel in A. It is that difference of force that brings the
mass from the distance ro+Dr
back to ro (after a quarter of rotation).
In the
case of the circular orbit having a constant radius ro,
the gravitational force is equal to the centrifugal force so
that the sum of the forces is zero. We have:
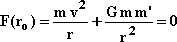 |
18 |
From equation 18, for the circular orbit ro, we have:
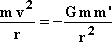 |
19 |
The
reason for which the mass traveling on the ellipse at location A
(figure 1), moves back to the orbit (toward the average radius ro)
is because its velocity had decreased previously, when the
distance increased from ro to ro+Dr. This is a consequence of
conversion of the total kinetic energy into gravitational
energy. When the ellipse passes at location A, the distance
from the Sun is ro+Dr.
Let us
calculate the change of force on the orbiting mass, as a function
of the distance from the Sun. There are two variables, v and
r. The derivative of equation 18 gives the change of force
as a function of the radius r and the velocity v. We get:
 |
20 |
At
location A, the gravitational potential has increased.
Therefore the velocity v must decrease. Knowing that the
total energy is conserved, let us calculate the change of velocity
as a function of the distance r from the Sun. The
relationship between the kinetic energy and the potential energy
is:
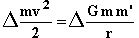 |
21 |
Let us
calculate the derivative of equation 21. The substitution of
equation 21 in its derivative, gives the relationship between the
change of velocity with respect to a change of radius when energy
is conserved. Equation 21 and its derivative give:
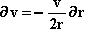 |
22 |
Therefore, the change of force calculated in equation 20 can now
be expressed as a function of one unique variable dr. Equation 22 in 20, and then
substituting equation 19, we get:
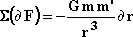 |
23 |
Equation 23 gives the change of forces bringing the mass back
toward ro. This is exactly the force involved in the
elliptical orbit passing through location A. This extra force
would transform the large circular orbit in A into the elliptical
orbit as illustrated on figure 2. Similarly, we find that the same
extra force must be applied in the opposite radial direction at
location B to bring the particle back to the initial external
radius ro (also illustrated on figure 2 and at location
B on figure 1). Then in that case, Dro
is negative. Consequently, this shows mathematically, that the
mechanism of translation of a mass around the Sun is such, that
for an ellipse, with respect to the corresponding circle, there is
a force bringing the mass back to the initial ro every
time a mass is deflected from its initial orbit.
Whether the mass moving on the elliptical path is "inside" or
"outside" the circle, the force always push the mass back toward
the circle ro. Furthermore, this force is
proportional to the distance dr, as
calculated above (equation 23). We must notice that this force has
the same mathematical form as the force of elasticity known as
Hooke's law. This force is responsible for the elliptical shape of
planetary orbits.
5 - Harmonic Oscillator.
What is
the behavior of a mass submitted to such a force, which always
brings back the mass toward the opposite side of the average
radius? According to equation 23, that force focuses toward ro,
all orbiting masses, with a force which is proportional to the
width of the shaded area illustrated on figure 2. In classical
mechanics, that force is characterized by the constant k,
(called the spring constant). It is a force per unit of
displacement (along the r-axis). The force of a harmonic
oscillator [2] is defined by the
relationship:
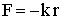 |
24 |
In
classical mechanics, we know that in order to produce a periodic
oscillation across ro, the value of k must be positive,
just as obtained above. This problem, well known in physics, has
been solved centuries ago and is recalled in numerous textbooks [2]. We know that a force is the second
derivative with respect to the distance r. We have:
 |
25 |
Equations 24 and 25 give:
 |
26 |
The
solution of equation 26 is a sine wave, oscillating on each side
of the central position ro. The period of oscillation
P(osc) is:
 |
27 |
Substituting the spring constant k existing on our elliptical
orbit as given above, equation 23 into 27 gives:
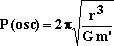 |
28 |
Equation 28 gives the period of oscillation P(osc) of the mass on
each side of the radius ro along a curve axis. It is
very important to notice that equation 28 has been obtained
independently of the time taken by the mass to complete a
revolution of 360 degrees around the Sun. Equation 28 gives the
period to complete one full oscillation across
either side of the average radius ro. That period of oscillation
depends on the spring constant k. It is completely independent of
the velocity of the mass along the orbit and of an assumed length
of a trajectory. However, the period of rotation (2p radians) of Mercury around the Sun at the
distance ro, depends on the circumference of that orbit
and the velocity of the mass on that trajectory. It is completely
independent of the period found above using the spring constant k.
6 - Comparing two Independent Periods; P(osc)
and P(rot).
Let us
now compare the time P(osc) taken by the mass to complete one
full oscillation on either side of the average radius ro
of a circla, and the time P(rot) taken by the same mass to
complete one full rotation around the Sun. In the calculation of
P(osc), we use the relationship (equation 28), giving the period
of oscillation of the particle across the radius ro.
Let us transform the parameters under the square root (in
equation 28) as a function of the velocity V of the mass moving
around the Sun. We know that the gravitational force Fg
around the Sun is equal to the centrifugal force Fc.
We have:
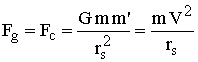 |
29 |
where rs is the radius of the orbiting
distance of the mass from the Sun.
Equation
(29) gives
 |
30 |
Equation 30 in 28 gives:
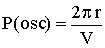 |
31 |
Equation 31 is the period of oscillation P(osc) of the mass on
either sides of the average radius ro. However, the
period of rotation P(rot) of Mercury around the Sun can then be
calculated independently, using a simple geometrical relationship.
From the relationship using the perimeter of the trajectory
divided by the velocity, we get:
 |
32 |
Equation 32 uses the circumference of a circle equal to the
perimeter of an ellipse having a small eccentricity. This is
demonstrated in appendix I of this
paper. Consequently, when we do not apply any correction for
mass-energy conservation, as done usually with Newton's equations,
we find that equations 31 and 32 show an extraordinary coincidence
between the period of oscillation P(osc) of a mass across the
average radius ro and the period of rotation P(rot) of
the same mass around the Sun. We have:
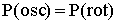 |
33 |
Let
us notice that such a coincidence would not exist if the
gravitational field around the Sun would not decrease exactly as
an inverse quadratic function. This has been shown in more detail
previously [1]. A difference would appear in
equations 23 and this would not lead to an equal phase
relationship between the periods of oscillation and rotation. This
is well known mathematically. Since these two independent periods
P(osc) and P(rot) are identical for the inverse quadratic force
existing around the Sun, the period of rotation around the Sun
coincides with the period of oscillation of the body across the
average radius ro as required by Kepler's laws and
observed experimentally. Therefore, the major and minor axes of
the ellipse are always pointing in a constant direction in space
as a function of time. The equality of the period between the
oscillation on both sides of the radius and the rotation around
the Sun is illustrated on figure 3. Both periods P(osc) and P(rot)
are the same.

Figure 3
The
result above has been obtained using the conservation of potential
plus kinetic energy but without mass-energy-conservation.
When energy (kinetic or potential) is given to a
mass, the mass of that energy is given to the mass having received
that energy, following the relationship E=mc2 as demonstrated
previously. Let us now take into account the principle
of mass-energy conservation.
7 - Fundamental Considerations.
In
physics, a natural description of the period of rotation is
given as the time taken by a body to complete one full rotation
by 360 degrees or 2p radians around
the Sun. We will see now that Newton's laws do not lead to a
perfect ellipse (without precession) when the principle of
mass-energy conservation is strictly applied. The fundamental
reasons have been explained in the book entitled Einstein's
Theory of Relativity versus Classical Mechanics [1]. The full
explanations and calculations are too long to be repeated here.
You find them explained in detail in the book [1]
but they are also available on the internet. Only a concise
description of the fundamental principles is recalled here using
some examples. The study of the original paper [1]
is indispensable for the complete understanding of the
phenomenon.
Let us
mention first that the principle of mass-energy conservation is
one of the most important fundamental principles in physics.
This principle is always valid and must never be neglected and
transgressed. This principle implies that we cannot create from
nothing and we cannot annihilate into nothing. Mass and energy
are two different aspects of the same constituent of matter.
Energy (E) always possesses mass (M) and mass always possesses
energy. Mass can be transformed into energy and vice versa. The
ratio of proportionality between mass and energy is a constant,
which happens to be equal to the square of the velocity of
light.
Serious
consderations in physics shows that when kinetic or
gravitational energy is given to a frame of reference, that
increase of energy increases the mass of the frame,
corresponding to the amount of energy given to the frame,
according to E=mc2.
Whatever the system of reference used in the energetic frame to
determne the standard references, we have seen that the local
reference standards of mass, length and clock rate change during
the passage from rest to the energetic frame. However,
that change of local reference standards are undetectable
locally in the moving frame, because matter forming the frame is
submitted to the same increase of energy as any other matter
used to do experiments inside the moving frame. Therefore,
after the acceleration of both, a frame and all local matter
used to do a local experiment, have increased their energy, and
therefore their mass. Therefore, locally inside the frame,
this is undetectable. This is required by the principle of
mass-energy conservation "between frames".
The
calculation of the Bohr atom, involving quantum mechanics is
also requires in that claculation, as demonstrated previously in
the book: Einstein's Theory of Relativity versus Quantum
Mechanics. For example, let us consider a grain of sand in
space moving around the Sun at the Mercury distance, having a
mass of one million atoms. When this grain of sand is moved from
Mercury orbit around the Sun to the Earth's distance from the
Sun (or about an infinite distance), we need extra energy to
move it against the gravitational potential of the Sun. The
extra energy can be obtained at the cost of transforming some
mass into energy. Suppose that, to provide the required energy
to raise the grain of sand from Mercury orbit, to Earth's
distance from the Sun, it is necessary to transform one atom of
mass "m" into energy (E=mc2).
We also assume that that extra energy (extra atom) is taken from
an external source near Mercury's orbit. Therefore the total
number of atoms leaving Mercury's orbit around the Sun is 1 000
000 (plus the equivalent energy of another one). Then, while the
grain of sand is moved away from the Sun, the energy of the
disintegrated atom is used up gradually (like "dissolved" into
the mass of the grain of sand), so that finally, the number of
atoms reaching the Earth distance is again one million, after
having transformed the energy of the atom into gravitational
(potential) energy.
Then
the total number of atoms is the same at Mercury orbit from the
Sun (which is 1000000 Mercury atoms plus energy) as at Earth
orbit from the Sun (which is agan 1 000000
Earth atoms). Therefore 1000001 atoms at Mercury orbit has the
same total mass-energy as one million atoms at Earth
orbit. The mass-energy produced from the disintegration of one
atom has been given to all other atoms. The logical explanation
implies that each atom has an extra mass-energy after reaching
the Earth orbit. They have a slightly larger mass than the
atoms at a lower potential energy on Mercury orbit. There
is no other way to satisfy the principle of mass-energy
conservation.
One can
see that the same relative change of mass-energy must also exist
on the standard reference kilogram used on Earth's orbit from
the Sun. The standard reference kilogram can be defined by an
absolute number of atoms. The standard kilogram simply contains
a much larger number of atoms than a grain of sand. The
principle of mass-energy conservation requires that one
Mercury-kilogram (at Mercury distance from the Sun) contains
slightly less mass-energy than the Earth-kilogram (at Earth
distance from the Sun), even if the number of atoms is exactly
the same. That change of mass of each atom is real. It is not an
illusion. This is required by the principle of mass-energy
conservation.
There
are several other logical consequences to that change of mass of
bodies, due to gravitational or kinetic energies. Since the real
physical mass of bodies changes when we add energy, one must
realize that particles, like electrons and protons of atoms,
forming those masses must logically also change their mass,
exactly in the same proportion as atoms. Furthermore,
using quantum mechanics [1], one can show
that a change of electron and proton mass modifies the length of
the Bohr radius. Due to that change of the Bohr radius, the
physical lengths of bodies and the energy of the quantum levels
change when gravitational or kinetic energy is added to a mass.
All these phenomena have been explained and calculated
previously [1].
Following the change of the Bohr radius, quantum mechanics also
predicts a change of quantum levels, due to the change of
electron mass, implying also a corresponding change of rate of
atomic clocks [1] . It is also
required that all matter, including organic matter and even
human bodies, function at a different rate when electrons
forming them have acquired or released some potential or kinetic
energies. Since Mercury in its orbit has a different
gravitational energy and possesses a different kinetic energy,
matter on Mercury (i.e. due to its Mercury distance from the
Sun) has a different mass. In addition, clocks on Mercury are
functioning at a different rate due to the change of electron
mass.
However, we have seen above that that change of mass, length and
clock rate is undetectable, because matter from this frame,
that forms the standards of reference in a frame, changes
in the same proportion as the local matter being investigated
inside the same frame. Consequenlty, the experimental
parameters (number of units) measured in the energetic frame are
identical to the ones in the initial frame, but they are not
coherent with the increase of mass-energy between the two
systems of reference. Since the increase of
mass-energy in the energetic frame is real, the numerical values
measured inside the energetic frame are not compatible with the
principle of mass-energy conservation and therefore are in
error. The relative size of the standard references must
be calculated. The relationships transforming the standard
units between locations at different gravitational potentials
and different velocities have already been calculated [1] . The length of the radius of the
orbit of Mercury is a number which is equal to the number of
Mercury-meters times the length of the local standard
Mercury-meter. However, that number is not equal to the number
of Earth-meters to measure the same orbit of Mercury, because it
is measured using the shorter Earth-meter. We must notice
that Newton's laws of physics deals with the numbers
that are fed into the equations. Since the number
of meters to measure the "same physical length"
(using the longer Mercury meters) is smaller than the number
of Earth meters, we must take that difference into account.
In
physics, there exist several systems of units using meters,
feet, kilograms, pounds, coulombs, statcoulombs, abcoulombs etc.
that have been devised in a coherent way so that the coherent
use of any set of reference units leads to answers which are
compatible, independently of any system of units. In fact, one
has a complete choice of systems of reference units that leads
to the same "physical" answer, although
represented by different numbers when using units having
different names. However, contrarily to the above, when we apply
the principle of mass-energy conservation between frames, the
units of mass, energy, lengths and clock rates in different
frames cannot be the same. Most importantly, the principle
of mass-energy conservation must be satisfied. The correct
calculation requires coherence between frame. Therefore
the local number of units must be corrected with respect to the
Earth value considered at infinity. We show here below, that
this logical correction explains perfectly the advance of the
perihelion of Mercury without any relativity principle.
In the
calculation below, for simplicity, we make the approximation
that the Earth is infinitely remote from the Sun.
Therefore we consider that the Earth is located in Outer
Space. The number of meters of the Earth from the Sun is
noted "NO.S. ". Corrections due to the residual Earth
gravitational potential can be easily done later. Furthermore,
when we say that a mass is near Mercury, one must understand
that it at a location near the Mercury orbit, assuming that the
gravitational energy due to Mercury is zero.
As
explained previously [1], since the number
of local units corresponding to local standards of length, mass
and clock rates are numerically different in different frames,
(due to mass-energy conservation) these different reference
standards must be clearly identified without ambiguity. A
special notation must identify clearly in what frame the unit is
calculated. Our notation uses a sub index to refer to the proper
units in use. Notation [meterM]
represents the "physical" length of the standard
Mercury meter, and [meterE] is
the "physical" length of the Earth meter.
Therefore these "physical" lenghts are local "etalons".
Also, [N-LengthM], is the
number of Mercury meters corresponding to the physical length [LM], and [N-LengthE]
is the number of Earth meters corresponding to the physical
length [LE]. For example, the
physical length (in Earth meters) of the radius of the orbit of
Earth is:
 |
34 |
Using Mercury meters, the same absolute physical length (distance)
is given by:
 |
35 |
Of
course, when we measure the same "realistic physical quantity", we
have:
 |
36 |
In
the above description, there is no
non-realistic concept like "space contraction". There is just a
real physical change of length of matter due to the change of
the Bohr radius, required by the principle of mass-energy
conservation.
Equations 34 and 35 can be used to measure any object
located on Earth, on Mercury or anywhere else having a different
kinetic energy or gravitational potential. Applying mass-energy
conservation, we have explained previously
(Chapter 5, equation 5.31 of [1])¸ that the
relationship between the Bohr radius of the atoms of the
Mercury-meter [meterM,v,] having a velocity v, and the atoms of the "Outer
Space" meter [meterO.S., 0, ]
with velocity zero, can give the relative lengths between the
two standard meters, one on Mercury with respect to another one
in Outer Space. Since we are able to determine the
increase of Bohr radius as a function of Gravitational and
Kinetic Energy, we are able to establish the relative "number"
of local meters between frames leading to the same real physicsl
length.
We
have
seen
in
the book: "Einstein's Theory of Relativity versus Classical
Mechanics" in Chapter 5, equation 5.31, that the relative length
of the standard reference meter between a meter (meterO.S. ) in outer space
and another one located in a gravitational potential at the
Mercury distance (meterM) from the Sun. That relationship 5.31 in
chapter 5 is:
 |
37 |
We have, [NO.S., 0] is the
"Number" of meters in Outer Space (when velocity is zero).
Also [NM,V,] is the number of
meters on Mercury when the velocity is V. Equation 37
gives the relative number of meters in each frame so that the
the same real length is represented in both frames. We
recall that equation 37 takes into account both, the increase of
potential energy due to the gravitational energy, and also the
change of kinetic energy (velocity) when a mass passes from the
Mercury orbit to a higher orbit. In equation 37, the
coefficient 3/2 to (Gm'/c2RM) is the sum of
the two phenomena explained in Ref, [1] Chapter 5. We have
shown that there is a component (Gm'/c2RM), which is the contribution due to the increase of
potential energy, while the component (1/2)(Gm'/c2RM) is the contribution due to the slowing down of the
velocity of the frame in a higher orbit.
Therefore,
the
change
in
the number of units in equation, 37 corresponds to the change of
the number of units of length taking into account the change of
gravitational potential as well as the change of velocity of an
orbiting mass at different distances around the sun. Here, for
simplicity, we can substitute the location of Earth with "Outer
Space", if we accept the approximation that the Earth is
sufficient close to outer space with respect to Mercury.
However, in order to obtain the exact change of number of meters
between the Earth orbit and the Mercury orbit, a remaining small
correction can be done with respect to outer space, if we
wish. Taking into account that we compare the "number"
[N-rE] of meters in a frame in
the Earth orbit located at a distance rE from the sun, with respect to the "number" [N-rM] of meters in the
frame located on the Mercury orbit at a distance rM from the Sun,
equation 37 becomes:
 |
38 |
We
have e is equal to:
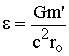 |
39 |
We have
[N-rE] and [N-rM] representing respectively the number of Earth and
Mercury meters to measure the same absolute length. We have
m' is the mass of the Sun, G is the Cavendish gravitational
constant, c is the speed of light, and ro is the
distance from the Sun. As a practical example for Mercury orbit, e is about 0.000 000 025, therefore e2 is always neglected in all calculations, in equations
and in all series expansions in this paper. As given by equation
38, the observer on Earth, measuring the same Mercury orbit but
using the longer Mercury meter, will feel that the distance from
the Sun is smaller, because the number of local meters [N-rM] needed to measure the same absolute physical length is
smaller.
8 - New Orbiting Velocity.
Classical mechanics predicts that the orbiting velocity of a
planet is larger when the number of meters measured from the Sun
to the planet is smaller. This is well known as Kepler's laws.
Using classical physics, we have seen that the kinetic energy of
an orbiting planet around the Sun is (minus) half the
gravitational potential (see equation 13). We have:
 |
40 |
The
potential energy is:
 |
41 |
The
kinetic energy is:
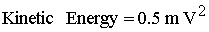 |
42 |
Therefore, from equations 40, 41 and 42 we have:
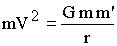 |
43 |
This gives:
 |
44 |
Let
us consider that we displace the orbiting mass by a small radial
distance dr. Using the derivative of
equation 44, we find that the required corresponding physical
change of orbiting velocity dV with
respect to the change of radius dr
is:
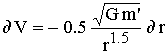 |
45 |
Substituting 44 in 45 gives:
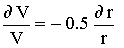 or or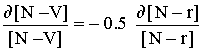 |
46 |
From equation 46, we see that when the number of radial units r
decreases (due to energy conservation), Newton's laws require that
the relative (number of units of) velocity increases by (minus)
half the relative change of radius. Using the principle of
mass-energy conservation, we have seen above in equation 38 that the number of Mercury-meters
[N-mM] is different from the
number of Earth-meters [N-rE]
(when measuring the same absolute length).
When an observer on Mercury measures the length of his orbit
around the Sun, he will measure it using his longer Mercury
meter. Therefore he will find a smaller "number" of
meters, than if measured by the Earth observer (who uses the
Earth meter). From equation 38, we find that that smaller
number of local meters on Mercury is given by the relationship:
| [N-rm]
=(1-1.5e)[N-rE] |
47 |
This
variation
of
the
number of meters can also be expressed as a fraction
representing the relative change of number of meters (between
the Mercury measurement and the Earth measurement) with respect
to the total number. Using equation 47, we have:
 |
48 |
The
Mercury
observer
also
wishes to measure the change of velocity of his planet using his
own units, and compare it with a measurement done by a remote
Earth observer. We have seen in equation 46 that the
relative change of velocity is minus half the change of
radius. Using that relationship, let us calculate the
relative change of velocity. Putting 48 in 46 gives:
 |
49 |
Let
us express that function as the "number" of meters. The
relative change of number of Earth-units of velocity with respect
to the number of Mercury-units of velocity, from equation 49
gives:
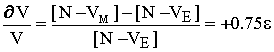 |
50 |
Equation 50 can also be written:
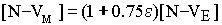 |
51 |
Let
us discuss the physical phenomenon implied in equation 51. We know that "locally", Newton's laws of
physics are always valid in all frames. For example, if the
Earth orbit would drift near the Sun at the Mercury distance, we
would still be submitted to exactly the same Newton's equations,
using the local units of length and time etc. . ..
existing on Mercury. Newton equations are always perfectly
valid locally inside all frames, on the condition that we
use local units. Therefore the solution
presented in this paper will be compatible with that fact.
However, using his local standard units of reference, and
newton's laws, his calculation will not be compatible with the
fact that there is an advance of the perihelion of the
elliptical orbit. For the Mercury observer, the perihelion
of the orbit is not local. The observer of Mercury must
modify the data obtained in his own observation in order to be
compatible with the fact that the line passing through the Sun
and his own planet is speeping the sky as a function of
time. Therefore the Mercury observer must use the correct
(Outer Space) standard units of reference, which are not the
standard units existing locally on his frame.
Let us us
now consider the length of the corresponding circular orbit.
Since Mercury travels at a higher velocity than previously
calculated with Earth units, the time taken by Mercury (period of
rotation) around the Sun is reduced. We see in equation 51, that
this period of rotation, giving the time taken to complete a
rotation of 360 degrees or 2p radians
around the Sun is shortened. However, in compatibility with the
principle of physical reality, there is a difference between the real
length of the trajectory to complete this circumference for an
observer using Mercury units and for an observer using Earth
units.
We will
see here that the advance of the perihelion of Mercury is due to
the fact that Mercury actually travels a longer path, (longer than
2pr) before the elliptical orbit is
closed (because we have applied Newton's laws combined with
Mercury units). We see below that due to the larger velocity
required by Newton's laws, using Mercury units, it takes a shorter
time to complete 360 degrees on the circumference of Mercury
orbit. We have shown above in sections 2, 3, 4 and 5, that
an ellipse corresponds to an oscillation on each side of the
curved axis of a circle. Using Earth units in both frames,
(which is wrong) when calculating the period of oscillation on
each sides of the ellipse in equation 31, we found in equation 33,
that it takes the same time to complete the oscillation on either
sides of the circle than the time to complete the rotation of 360
around the Sun. However, using the number of Mercury units,
corresponding to the same physical length, we will see below that
it takes a different time to complete the oscillation on either
sides of the circle (equation 31) than the time to complete the
rotation of 360 around the Sun.
9 - Taking into Account Mass-Energy
Conservation.
Let us
apply equation 28 to the classical units existing on Earth. We
have seen that the period of oscillation of Mercury on both
sides of the average radius ro calculated by an
observer on Earth would be calculated as:
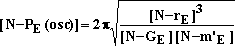 |
52 |
In
equation 52, the physical quantities have been substitued by the
corresponding "number" of units. However, this equation
cannot be applied without corrections, because this equation uses
masses (and all other units) as they exist on Earth, while the
interacting mass with the solar gravitational field is different
at Mercury orbit (as mentioned above). We recall that the sub
index E (as in PE) means that
the units used are the ones existing far from the Sun where the
principle of mass-energy conservation does not require
correction. From equation 37, we can see that on Earth, the
standard meter is shorter than on Mercury. Therefore, the number
of Earth-meters [N-rE] is larger
than the number of Mercury-meters [N-rM], when measuring the same physical length. We
have:
 |
53 |
In
equation 39, we have:
 |
54 |
We know
that G is an absolute physical constant. However, since the
standard units existing on Mercury are different from the standard
units on Earth, different numbers will then express the same
physical gravitational constant G. The gravitational force
at one point is physically the same, independently of the units
used by the observer. However, the number of units to
describe it will be different, since the reference units are
different, but this will represent the same field and the same
physical force. Therefore we have to calculate the
relationship giving the change of the number of local units of the
gravitational constant G due to the change of standard units on
Mercury in compatibility with the principle of mass-energy
conservation. The change of the number of units [N-G] of G has
been calculated previously ([1] Chapter 4 Equation
4.65) in the case of zero velocity. We
must then compare the numerical value of G when two conditions are
changed simultaneously. One is due to the physical change of
velocity as given in equation 51. The other is a mathematical
transformation, because we have to express the very same physical
quantity using different standard units (from Earth units to
Mercury units).
Let us
calculate the relationship between the number of gravitational
units [N-GM], and [N-GE], resulting from those two changes. This can be done
using the relationship giving an equal force between the
gravitational force and the centrifugal force. Since the
centrifugal force must always be equal to the gravitational force
using proper values, we have in all frames, (when using proper
units):
 |
55 |
This is mathematically equivalent to:
 |
56 |
Let
us use the correct notation showing the number of
units. To get the correct physical answer, one must use the number
of Mercury-units, since it is the relevant number of units
existing at the location where the phenomenon takes place.
The change of the number of units of G can be calculated using the
relationship 56 equals to G. Using the notation, and taking
into account the number of units leading to the same quantity,
equation 56 should be written:
 |
57 |
Let
us compare this number [N-GM] in
Mercury units, with the number [N-GE] of units of G on Earth. On Earth, the relevant number
of units is:
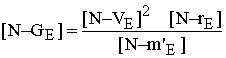 |
58 |
Due
to the physical change of velocity given by equation 51, we have
seen that:
 |
59 |
From equation 37 when we measure the same physical length, we find
that the change from the number of Earth-meters [N-rE] to the number of Mercury-meters due only to
mass-energy conservation gives:
 |
60 |
Since we are using Mercury units, let us now calculate the solar
mass. We want to determine the number of Mercury
kilograms required to be equal to the mass of the Sun. However,
the Mercury kilogram has to be given as a function of the Earth
kilogram, which is assumed at rest and sufficiently far from the
gravitational potential of the Sun. Therefore, the number of units
of Mercury-kilograms will be different from the standard Earth
kilogram, because the Mercury kilogram is located deeper in the
gravitational potential of the Sun and furthermore because of its
velocity.
The
change of the number of Mercury kilogram [N-mM] , to measure the solar mass, instead of the Earth
kilogram, is calculated in the following way. Due to the
gravitational energy, the Mercury kilogram (at rest) is smaller
than the Earth kilogram (at rest). Due only to gravity, equation:
(see [1] chapter 4 equation 4.42)gives:
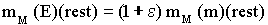 (Due only to gravity) (Due only to gravity) |
61 |
Where the indexes (E) and (M) give respectively the location of
the mass on Earth or on Mercury. Here those masses are expressed
in Mercury units (using the sub-index "M"). In addition, we know
from Newton's laws, that the kinetic energy of an orbiting mass
around the Sun is half the (negative) gravitational potential
energy. Consequently, the kinetic energy of Mercury gives a larger
mass on Mercury (expressed in Mercury units) than at rest (always
on Mercury):
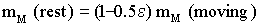 |
62 |
Combining equations 61 and 62, we find that the relative mass of a
Mercury-kilogram in motion [mM(m)(moving)]
with respect to an Earth-kilogram at rest on Earth [mE(E)(rest)]
is (expressed in Earth units):
 |
63 |
Therefore, the moving standard Mercury kilogram is slightly less
massive than the standard Earth kilogram at rest when common units
are used. However, the quantity required is different. It is
the number of Mercury kilograms to equal the mass
of the Sun. Of course, the absolute mass of the Sun does not
change because it is measured with respect to the Mercury moving
kilogram. However, the number of Mercury kilograms
that represents the Sun will be different. From equation 63, we
can deduce that the number of Mercury-kilograms in
the Sun is larger than the number using
Earth-kilograms according to:
 |
64 |
We can
now calculate the number of gravitational units [N-GM]. Putting 59, 60 and 64 in 57 gives:
 |
65 |
Always neglecting e2 and higher powers of e with
respect to e , equation 65 is equal
to:
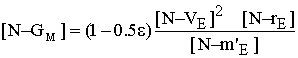 |
66 |
Using equations 66 and 58, we get:
 |
67 |
We
have taken into account that the absolute physical value of the
universal gravitational constant G never changes. However, since
it is now measured using Mercury units, its numerical value has
changed. Furthermore, we have seen that the velocity (equations 51
and 59) of Mercury has changed. Equation 67 has taken these two
phenomena into account.
Let us
now calculate the period of oscillation on each sides of the
radius ro. Substituting 60, 64, and 67 in 52, we get:
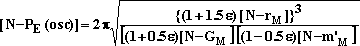 |
68 |
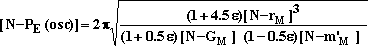 |
69 |
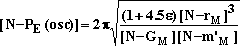 |
70 |
The
period of oscillation of Mercury calculated with Mercury units is
then:
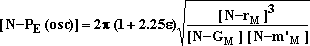 |
71 |
Similarly to equation 52, we can easily formulate the period for
the Mercury observer. Combining equation 51 with 71 gives:
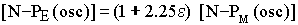 |
72 |
Equation 72 gives the period of oscillation [N-PM(osc)] of Mercury on either side of the average radius
with respect to the initial period of oscillation [N-PE(osc)] using Earth parameters (from infinite distance).
We have seen that [N-PE(osc)] is
the period when mass-energy conservation is not considered (or
when we are at a near infinite distance from the Sun and with near
zero velocity). However, since the period of oscillation [N-PE(osc)] without mass-energy corrections is identical to
the (initial value of) period of rotation (see equation 33), then
equation 72 shows the increase of period with respect to a fixed
direction in space.
10 - Relative Distance Reached after One
Rotation and One Oscillation.
We have
seen in equation 51 that, in order to satisfy Newton's physics
with the local parameters, Mercury must travel more rapidly on
its orbit according to the relationship:
 |
73 |
Even if Mercury travels more rapidly on its orbit, the length of
the perimeter of the orbit to complete 360 degrees or 2p radians does not change. Consequently,
the length traveled by Mercury to turn 360 degrees around the Sun
does not change even if the velocity is increased.
However,
we have seen in equation 72 that due to the change from standard
Earth units to standard Mercury units, Newton's equations give a
longer period of oscillation of Mercury (longer time) on either
side of the average radius ro. Due to that longer
period of oscillation, Mercury will travel a longer distance
before closing the ellipse. Furthermore, since the physical
velocity V of Mercury is larger (due to mass-energy conservation)
as seen in equation 51, the distance traveled on the orbit becomes
longer due to the increase of period, but also due
to the increase of velocity. Let us compare the
distance traveled by Mercury to complete one full rotation by 360
degrees with the distance traveled to complete an oscillation,
which closes an elliptical orbit. The distance traveled when
completing one oscillation is:
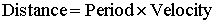 |
74 |
We
have seen that due to the use of Mercury units and the local
agreement with Newton's laws (using proper values), the real
physical velocity of Mercury is larger according to equations 51
(and 59). The corrected velocity [N-V(corrected)] with respect to
the non-corrected velocity [N-V(non-corrected)] is:
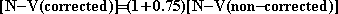 |
75 |
Similarly, as demonstrated in equation 72, due to the change of
standard units on Mercury, the same physical forces measured with
the Mercury units, lead to a slower period of oscillation across
the average radius ro. This
gives:
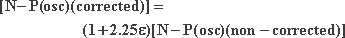 |
76 |
The
correction of length needed to close the elliptical orbit is given
by the parameters corrected for mass-energy conservation. Equation
76, written correctly becomes:
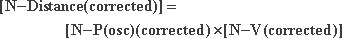 |
77 |
Substituting equations 75 and 76 in 77, we get:
 |
78 |
Taking into account that e is
extremely small, we neglect the second order term (e2). Equation 78 becomes:
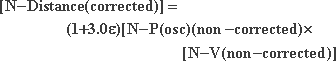 |
79 |
This
is
also
equal
to:
 |
80 |
Let
us note that the relative change of distance of equation 80 (or
relative change of angle) is the same whether we use Mercury
meters or Earth meters (we neglect higher orders in e2).
The indexes E or m are useless since the increase of angle a is the same in both frames, as expected
logically. Equation 80 is illustrated on figure 4.

Figure 4
On figure
4, the circumference of the orbit is unrolled at the average
radius ro (circle) and forms the "Distance" axis. We
have seen that the circumference of the orbit is not changed since
Mercury orbits around the Sun is calculated at the same absolute
radius ro. However, the real distance traveled by
Mercury during one full transverse oscillation is longer than the
translation of 360 degrees, due to the slower oscillation on each
sides of the radius ro and the increase of velocity
resulting from the use of Mercury parameters. This explains the
advance of the perihelion of Mercury.
Let us
compare equation 76 with Einstein's predictions and astronomical
observations. From equations 38 and 80 we get:
 |
81 |
Equation 81 shows that the advance of the perihelion of Mercury,
calculated above with a small eccentricity is mathematically
identical to equation
5.45 in section 5.10 of [1]. Without the second order
e2 for the eccentricity, in the
case of Mercury, this leads to an accuracy of 96%. Taking
into account the second order e2
for the eccentricity, the non-linear change of gravitational
energy adds a small correction, which is now taken into account.
It has been previously demonstrated [1] (section 5.10) that
the expression (1-e2) must then
multiply the denominator of equation 81, because the gravitational
potential is not linear between a small and a larger elliptical
orbit (taking into account the second and higher order terms).
This previously demonstrated phenomenon [1] (section 5.10) is
not repeated here, but it is easily applied to equation 81.
The final
equation then gives the change of distance to close an elliptical
orbit, with respect to a rotation of 2p
radians. Using equation 81, expressed as a function of the angle
of precession Df per century,
and a larger eccentricity e explained in section ([1]
(section 5.10). We find that this gives [1] (equation 5.45):
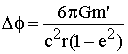 |
82 |
Equation
82
is mathematically identical to Einstein's equation. Therefore,
this shows that the advance of the perihelion of Mercury can be
fully predicted using only classical mechanics, without any of
Einstein's hypothesis and without space-time distortion. Neither
new physics nor any mathematical hypotheses have been used in the
above demonstration. Everything is now logical, realistic, and
based on mass-energy conservation.
11 -Illustration of the Advance of the
Perihelion of Mercury.
Figure 5
illustrates "in perspective" the periodic rotation of Mercury
around the Sun. It shows the precessing elliptical orbit of
Mercury (dotted curve) oscillating on both sides of the circular
orbit at ro (solid line), while the Sun moves uniformly
to the right hand side of the figure. The use of the standard
Mercury units reduces the number of units representing the force
(spring constant) which always pulls Mercury back toward the
average radius ro. Therefore, the period of oscillation
is longer. Then, the oscillation is not completed (ellipse not
closed) when Mercury has already completed a full rotation (360
degrees) around the Sun. We see that the ellipse is crossing the
circle upward (at ro) after more than one geometrical
rotation of 2p radians. The upward
crossing between the elliptical orbit (dotted line) and the
circular (solid line) line is repeated only after a supplementary
rotation angle a (after each 2p radians).

Figure 5
Figure
5 shows this cumulative advance a
after several rotations. The cause of the advance of the
perihelion of Mercury is now perfectly explained. We see that
this demonstration has been done using Newton's physical laws
instead of non-realistic mathematical models. This paper shows
the beauty and the universality of Newton's laws in Galilean
coordinates. Those laws are valid internally, everywhere inside
all frames when we use proper values. We msut recall that the
basic principle of mass-energy conservation has also been
foreseen by Newton [3].
It has
been reported that Einstein said: Since the mathematicians
have invaded the theory of relativity, I do not understand
it anymore [4]. It is the
author's wish that the realistic physical explanations presented
in this paper will never be drowned into the mathematics.
12 - Acknowledgments.
The
author wishes to acknowledge the helpful encouragement of Mr.
Bruce Richardson. Stimulating questions were also appreciated from
C. Couture, S. Talbert, I. McCausland, T. Phipps and T. Durt.
<><><><><><><><><><><><>
Appendix I
Description of an Ellipse with a Small
Eccentricity.
On order
to get a physical description of the transformations of a circle
into an ellipse with a small eccentricity, we must examine the
fundamental properties of ellipses. There is a general belief that
a circle becomes an ellipse simply by flattening the circle. It is
not realized that for a small eccentricity, an ellipse is much
better described as a circle in which the center of forces is
shifted away from the center. The flattening of the circle appears
only as a second order in a series expansion as demonstrated here.
Let us start with a fundamental property of ellipses. One of the
definitions of an ellipse [5] given by Brink
is:
An ellipse is defined as the locus of a point
the sum of whose distances from two fixed points (the foci) is
a constant.
From this
property of an ellipse, gardeners and others often construct
ellipses by driving pins at the foci and running a loop of string
around both pins, leaving a certain amount of slack. A marker P is
then placed inside the loop and moved around in such a way as to
keep the string taut. Since the amount of slack is constant, the
sum of the distances of the marker from the foci is constant, and
the marker traces out an ellipse. Such a construction is
compatible with the exact definition of an ellipse given by Brink
[5].

Figure 6
Figure
6 shows an ellipse with a large eccentricity. The distance "a"
is the semi-major axis and b is the semi-minor axis. The
eccentricity e is given by the relationship:
 |
A-1 |
It
has also been demonstrated that an elliptical orbit illustrated on
figure 6, corresponds exactly to the orbit of a body for which the
center of forces (here the Sun at F1) occupies one of the foci. This elliptical shape is the
one followed by most comets. Let us examine the way an orbit is
gradually transformed from a circle to an ellipse. First, when the
eccentricity increases, and before the circular shape of theorbit
gets noticeably flatter, the center of forces (focus F1 where the Sun is located) drifts from the center of the
original circle C to the left focus at F1. For a large eccentricity, the minor axis 2b then
starts to decrease with respect to the major axis 2a, as the
square of the displacement of F1.
Figure 6 above illustrates a large eccentricity. In the case of a
small eccentricity, this is studied using figure 7.
Figure 7
also illustrates the locus of a moving point P for which the sum
of the distances from the two foci (F1 and F2) is constant.
When the distance between the two foci is zero, we have a circle
and the two foci are superimposed at the same central location.
The radius of that circle is R. Let us move foci F1 to the left-hand side by the amount Dx (from C to F1). We see on figure 7, that when the length of the
string is kept constant, (equal to two R) the sum of the distances
F1-S1-F2 does not change
when Dx increases. The focus F2 moves always in the opposite direction and by the same
amount as F1.
We also
find the same constant total distance F1-S3-F2 on the left-hand side when the point moving on the
ellipse is at S3. In that case,
the major axis (in the horizontal direction) of the ellipse is
constant (equals 2a) for any eccentricity, when the foci are
shifted more apart.

Figure 7
Let us
now calculate the length of the (vertical) minor axis (2b) as a
function of the shift (Dx) of
the focus F1. The length of
the string passing through F1-S2-F2 is equal to the
length F1-S1-F2 (which is equal
to the major axis). Consequently, using the triangle F1-S2-F2, formed by the string, the semi major-axis "a" is
constant while the semi-minor axis "b", (the distance S2-C), is equal to:
 |
A-2 |
Using
a
series
expansion
for ArcSin and Cos, equation A-2 gives:
 |
A-3 |
In
that series expansion, there exists no term with power one of Dx/a. Since Dx/a
is infinitesimal in the problem studied in this paper, the
correction for the change of "b" as a function of Dx (which is a quadratic function
(second order)) is insignificant. The flattening of the trajectory
is observable only for a large value of Dx/a.
This shows that for a small displacement Dx
of the focus F1 with respect to
the center of the orbit, the minor axis does not change
appreciably with respect to the major axis and the original orbit
remains practically circular, even when the center of forces has
moved considerably apart (by Dx),
as seen on figure 7.
Let us
consider a numerical example. An elliptical orbit, at an average
distance of about 50 million of kilometers from the Sun, and
having an amplitude of oscillation of one kilometer with respect
to the exact circular orbit, implies that the Sun is one kilometer
away (value of Dx) from the
central circle. From equation A-3, (and other calculations) we can
also show that in that case, the major axis has not changed at all
and that the change of perimeter of this elliptical orbit, with
respect to the circular orbit is surprisingly small. For such an
astronomical orbit, for Dx
equals one kilometer, the change length of the perimeter is only
about 0.01 millimeter. This second order correction is clearly
negligible. Of course, for a large eccentricity, the corrections
imply other corrections due to the principle of mass-energy
conservation. However, they are irrelevant here but they have been
taken into account later in this paper in equation 78 and in the
original paper on the subject [1].
This
conclusion is also very important because in section 10 we had to
calculate the perimeter of an ellipse having a small eccentricity
(a first order series expansion). Consequently, we see now that
the first order series expansion contains no first power term.
Therefore in that case, the perimeter of the ellipse with a small
eccentricity is equal to the circumference of the circle.
<><><><><><><><><><><><>
13- References.
[1A]
Die Räumliche und zeitliche Ausbreitung
der Gravitation. Von Paul Gerber. Zeitschrift für
Mathematik und Physik Vol.
43, Pages 93-104 (1898).
Also: Paul Gerber, Die
Fortplfanzungsgeschwindigkeit der Gravitation, Annalem der
Physik, Vol 52, p. 415-444, 1917 (*)
[1] P. Marmet, "Einstein's Theory of Relativity
versus Classical Mechanics", Ed. Newton Physics Books, 200
pages (1997), Ogilvie Rd. Gloucester, On. Canada, K1J 7N4, also on
the internet at the address: http://www.newtonphysics.on.ca/einstein/index.html
[2] R. P. Feynman, The Feynman
Lectures on Physics, Vol. 1, chapter 21, Addison-Wesley Pub, Co.
1963.
[3] P. Rowland, "Newton and the
Concept of Mass-Energy" Department of History, University of
Liverpool, Liverpool University Press, P.O. Box 147, Liverpool,
L69 3BX (1990).
[4] Meta Research Bulletin,
Editor's note, 3, 1 (11) 1994, P.O. Box 15186, Chevy
Chase, MD, 20825-5186, USA.
[5] R. Brink, Analytical Geometry,
Ed. D. Appleton-Century Company Inc. New York, P. 217 (1935).
[6] P. Marmet, "Absurdities in Modern Physics: A
Solution" (1993), Ed. Les Editions du Nordir, c/o R.
Yergeau, 165 Waller St. Simard Hall, Ottawa, On. Canada K1N 6N5.
[7] Sagnac, M. G. J. de Phys.
1914, 4, 177-195.
[8] A. G. Kelly, "The Sagnac
Effect and GPS Synchronisation of Clock-Stations" International
Meeting: Galileo Back in Italy, Bologna, Italy, May
26-29 1999.
<><><><><><><><><><><><>
Return to: Top of Page
Return to: List of Papers on the Web
If you read this paper after chapter six of the Book: Einstein's Theory of Relativity
versus Classical Mechanics
you return to chapter seven at: Chapter Seven
About the Author
Contact e-mail
address.
<><><><><><><><><><><><>
This paper on the Web is a
revised and corrected version of the original paper.
---
This paper has been published under the title: "Classical
Description
of
the
Advance
of the Perihelion of Mercury" in Physics Essays Volume 12, No: 3,
1999, P. 468-487.
---
This paper has been presented at the International
Meeting: "Galileo Back in Italy II" Bologna Italy,
26-30 May 1999,
Title: "Einstein's Mercury Problem Solved in
Galileo's Coordinates" .. This paper is printed in the
proceedings: "Galileo Back in Italy" Istituto di
Chimica, "G. Ciamician", Via Selmi 2 - Bologna, Italy. P.
352 to 359.
---
This paper has also been presented as an invited
speaker at the meeting of the Society for Scientific
Exploration at Albuquerque, June 3-5, 1999. The title
is: "A Logical and Understandable Explanation to the Advance
of the Perihelion of Mercury"
<><><><><><><><><><><><>
Return to: Top of this page
Return to: List of
Papers on the Web




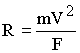

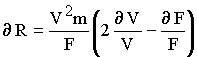
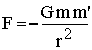


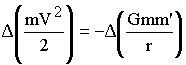


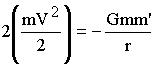
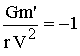
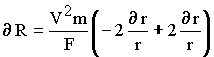
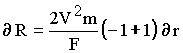 which is
which is