| 1 |
This paper was written when the author was at:Return to: List of Papers on the WebGo to: Frequently Asked Questions
Abstract
An
unexplained center-to-limb variation of solar wavelength has
been known for 75 years. Many theories have been developed
in order to explain its origin. Although recent studies
reveal a large amount of new information on the solar
chromosphere, such as asymmetries of lines and various mass
motions in granules, which lead to wavelength shifts, no theory
can consistently explain the observed center-to limb variation.
It is shown that the theory considered in this paper not only
explains this variation but also predicts its amplitude without
the use of any adjustable parameter.
1. Introduction.
The
dedication of a Special Issue of this Transaction to Hannes
Alfvén is a well-deserved acknowledgment for his extraordinary
discoveries [1],
which have demonstrated the importance of plasma in the
universe. Alfvén's works led to the discovery of
intergalactic plasma (matter) as the cause of the "cosmic
static" observed by Reber [2]. Intergalactic matter is expected to produce
inelastic transmission (redshift) when electrodynamical
(bremsstrahlung) considerations are taken into account [3]-[5]. It has been shown
[3], [5] that the amount of matter
calculated by Reber [2] is equal to the amount of matter required
theoretically [3], [5] to produce a red shift equal
to the Hubble constant. That same red-shift theory [3], [5] also leads to other verifiable predictions when
radiation crosses the solar chromosphere. In that case, a
center-to-limb variation (CLV) of solar lines is predicted, as
seen below.
The
center-to-limb variation of solar lines was reported at the turn
of the Century by Halm [6] and Adams [7]. About 200 papers have appeared on the subject since
then. The impressive number of independent observations
and discussions by Adam [8]-[10], Finley-Freundlich [11], Schröter [12], Struve [13], Higgs [14], [15],
Salman-Zade [16],
Snider [17],
Schatzman and Magnan [18], Pecker [19], Beckers and Cram [20], Reboul [21] and many others, including extensive recent
documentation of his unexpected phenomenon, plus the fact that
there has been no contradicting observation of the red shift of
the FeI lines, have firmly established that the wavelengths of
the Fraunhofer lines in the solar spectrum are dependent upon
distance from the solar limb. This CLV cannot be a
consequence of relativity, which predicts that all solar line
must be red shifted by a factor of 2.12 ´10-6 and hence should
be independent of the position on the solar disk. This CLV
is detected superimposed on the known Doppler shift resulting
from the relative motion of the Sun and Earth. During
those past years, observers hoped in vain to discover new facts,
but the basic observations of the CLV have not changed in 70
years, as is stated by Howard et al. [22] and Dravins [23]: "The early measurements of Evershed and
Royds [24] could adequately resolve differential line
displacements and more recent photoelectric instruments
yield practically identical curves".
The
object of this paper is to describe and assess the results of
exact computations according to some models, and to compare them
with experimental data. One of the models considered here
follows the hypothesis that the CLV is caused by Doppler shifts
due to radial mass motion in the solar photosphere and
chromosphere [13], [25] or to granules, as
calculated by Schatzman and Magnan [18], Cavallini et al. [26], Gurtovenko et al. [27], Adam et al. [28], Brandt and Schröter [29], Becker and Nelson [30], Kaisig and Durrant [31], and others. The model applied here and
calculated by Marmet [3]-[5] is based on the fact that the momentum transfer of
the solar photons, to the electrons of the atoms of the solar
atmosphere, produces secondary radiation due to
bremsstrahlung. The energy of this bremsstrahlung
radiation is taken away from the energy of the initial photons
and leads to a red shift. Such an energy loss is a natural
phenomenon, which has been described recently by Marmet [3]-[5]. No adjustable
parameters are used, and all constants are either fundamental
physical constants or well-known solar phenomena.
II. The Current Situation.
Measurements
of solar lines (sodium D-1 and potassium 7699Å) have been made [32], [17], and [25].
Initially, [17]
reported a disagreement with the gravitational red shift.
Two years later, Shider [25] claimed agreement with the gravitational red shift
following selection of his data (Earth motion smaller than
-12mA). The absence of any CLV as observed and explained [25] is due to the fact that
some lines "originate above that region of the
photosphere."
Many other exotic explanations, such as photon
decay [20], nonzero
photon rest mass [19],
and others, have been considered in order to explain all the
observed characteristics of the red-shifted Fe I lines.
Observations
[14], [15], [33] (and by others) have definitely determined that the
red shift of the lines near the limb is larger than the value
predicted by relativity and is accompanied by an asymmetry of
the lines profiles. Granules have been observed in the Sun
for some years, but this phenomenon has been unsuccessful in
explaining the CLV. More recently, it has been confirmed [23] that there is an upward
mass motion in the brighter granules, and a downward motion in
the darker intergranular lanes. The most recent data [34] yield simultaneous
resolution in both time and space in individual granules in
several spectral lines, determining the exact mass motion in
granules.
Accurate
new measurements [35]
led to the belief that there was meridional flow on the solar
surface. Again, it was hoped that such meridional flow
could contribute to the explanation of the CLV shift. More
recently, in two different papers, Cavallini et al. [26], [33] have shown that when several spectral lines are used,
their data do not fit with the sometimes-observed equatorward
mass motion that gives "anomalous CVL" and "contradictions".
Cavallini et al. [26], [33]
state in their last article that "these contradictions
somewhat reflect the contradictory results obtained in
previous measurements by other authors. This shows
that a line-dependent unknown phenomenon introduces a
latitude differential shift which is assumed as due to a
mass motion".
There
are different depths of comprehension of a physical
phenomenon. After a reasonable number of observations, one
normally tries to explain results (in this case CLV) in terms of
previously known phenomena such as relativity, mass flow,
granules, erroneous measurements, etc. When these attempts
are unsuccessful, it is useful to make some data analysis and to
compare the data with series of functions for which one can fit
arbitrary adjustable parameters. Due to the lack of a
working theory, such a "parametrized model" has
been used [23], [36] to fit the CLV
experimental data. This mathematical model provides a good
description of the data, but gives no real physical
understanding of the phenomenon.
The polynomials fitted by Bruning [36] and Cavallini et al.
[26], [33] are
| 1 |
III. Calculations
Calculations
based on the theory which takes bremsstrahlung into account are
considered first. In this case, Marmet [3], [5] has shown
that when a photon encounters an atom or molecule, the energy of
the transmitted photon is very slightly reduced. This
follows from the fact that a secondary photon of extremely low
frequency is emitted [3], [5] which
reduces very slightly the energy of the primary photon.
The
fact that photon scattering is always inelastic has also been
found independently and was demonstrated several years ago by
Bethe and Salpeter [41], and has been recalled more recently by Jauch and
Rohlich [42].
Because the energy loss is extremely small and the quantitative
amount of energy loss is difficult to calculate, this mechanism
has been generally ignored. One can see that, due to
bremsstrahlung, this inelastic scattering leads always to an
energy loss, and, consequently, the transmitted photon loses
some energy. Therefore, the photon is slightly red
shifted. It is seen that the energy loss is caused by the
acceleration of an electric charge (and therefore follows
Maxwell's equations) rather than by a quantum or a relativistic
effect. Quantum and relativistic considerations do not
lead to energy losses in this case. Since calculations of
energy losses due to the acceleration of charges is treated by
electrodynamics, we have used here classical electrodynamical
considerations. The results of those calculations have
been reported [3], [5]. It is seen that the
red shift produced depends on the number of collisions with
atoms and therefore on the amount of gas crossed in the
trajectory of the photon.
In order to calculate the energy loss (red shift)
produced when photons cross the solar atmosphere, we must first
determine the amount of gas above the base of the
chromosphere. By definition, the height of the solar limb
is the base of the chromosphere. The solar gas
density is known and given [43] as a function of altitude.
The
total amount of gas that the radiation has to pass through
before reaching the Earth is integrated from different altitudes
in the solar chromosphere. Thus, one obtains the column
density, which is the number of atoms in a column having a unit
cross section and a length equal to the distance between the
point where the absorption takes place and the observer on
Earth. A second factor takes into account that, for
different radii between the center of the disk and the solar
limb, the column density increases according to the secant of
the angle between the line of sight and the solar radius to the
point where the line of sight cuts the surface. Finally,
the solar curvature for the radiation tangent (or near tangent)
to the solar disk at or near the limb is also taken into
account. This last consideration makes the path length in
the solar chromosphere become finite at the limb. In
practice, we have found that this last correction adds a term
that has a negligible contribution for our purpose and is
limited by the experimental resolution near the solar limb.
The
amount of red shift produced by the collision of one photon on
an atom is given by b. This
parameter is called R in previous papers [3], [5].
It is seen that each time a photon meets an individual hydrogen
atom or molecule on its path, the initial photon loses a very
small fraction b»10-13 of its initial energy due to bremsstrahlung due to
momentum transfer on hydrogen in the solar chromosphere.
This is consistent with the prediction of quantum
electrodynamics as calculated by [42] and [41].
This
small energy loss [3],
[5] is based on the
following principles.
1)
In the scattering process between electromagnetic radiation and
atoms or molecules, one usually considers only the radiation
emitted by the transverse dipole induced by the polarizing
radiation.
2)
It is seen that when electromagnetic radiation is transmitted
through gases, the momentum transfer produces an axial dipole
following momentum transfer.
3)
This axial momentum transfer to the electrical charges
(electrons) of the atoms of the medium also produces
bremsstrahlung, which is completely perpendicular (orthogonal)
to the conventional scattering process (transverse
polarization).
4)
Marmet [3], [5] has shown that this
bremsstrahlung removes a fraction b
of the energy of the initial photon.
We
must realize that quite generally, when we deal with any waves,
a wavetrain always necessarily possesses at least two frequency
components. The frequency no measured usually,
is related to the rate of change of the electric and magnetic
field. However, since electromagnetic waves never last
during an infinite time, the oscillating wave amplitude finally
dies out after the time of coherence. Therefore, since the
amplitude of the wave must decrease to zero after a time
interval Dt related to the time of
coherence, (which is usually much longer than the time of one
fundamental cycle), this gives the very low frequency nc
(related to the time of coherence) component of the
wave. It is that very low frequency component, which
is responsible for the new Non-Doppler redshift [3], [5] and which has always been neglected in the
past.
In
the case of blackbody radiation, the relative energy b is given by:
 |
2 |
| 3 |
| 4 |
| 5 |
Since the red shift (Dl¤l) per collision is b, one finds that the total red shift is equal to:
|
|
6
|
|
|
7
|
|
|
8 |
|
|
9
|
|
|
|
|
10
|
|
|
11
|
|
|
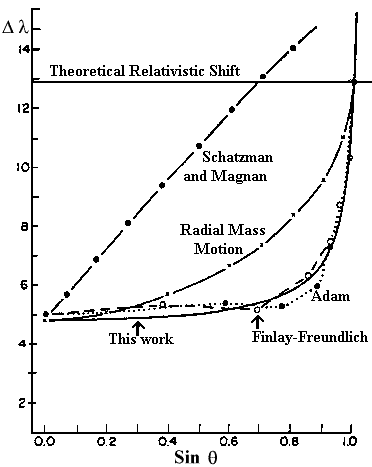

Figure 2
Fig. 2. Limb effect of solar lines as a function
of equivalent radial velocity.
IV. High-Pressure Phenomenon
A.
Multi-Atom Interaction
We have seen that the red shift of spectral lines
on the sun starts as expected at an altitude just below the one
of maximum absorption of these lines. This altitude (277
km) above the base of the chromosphere has also another
important characteristic - it sets a threshold to a
high-pressure phenomenon. As stated previously [5], one can see that when the
length of coherence of electromagnetic radiation is longer than
the distance between atoms of the gas, one single wave train of
radiation (one photon) has the possibility of interacting
simultaneously on more than one atom. In other words, one
single wave train can polarize several atoms simultaneously, and
the photon momentum is transferred to several electrons
simultaneously.
For
example, in the case of radiation interacting simultaneously on
a pair of electrons (located on different atoms), the total
energy emitted by bremsstrahlung by the pair of electrons that
has received a given momentum is smaller than the bremsstrahlung
emitted in only one electron (therefore half the mass) has
received the same total momentum. This is the consequence
of the Larmor law of radiation that says that the amount of
energy radiated by bremsstrahlung increases linearly with the
charge accelerated, but quadratically with the acceleration
given to the charge. Consequently, it is only in the case
when the gas density reaches low value, such that the length of
coherence is smaller that the distance between the atoms of the
gas, that one can be sure that only one atom interacts at a time
and that the red shift produced follows (10). Above that
critical pressure, the red shift (per collision) becomes smaller
and must practically disappear at a much higher pressure.
This means that a photon-atom interaction leads to the emission
of a smaller amount of bremsstrahlung when other atoms are
located within the coherence length of the interacting atom.
B. Critical Pressure
It
is very difficult to determine precisely the critical pressure
above which bremsstrahlung is no longer emitted a full
intensity. One can see [5, fig 1] that
the time of coherence Tc of blackbody radiation at half
intensity is given by the expression
|
|
|
|
C. Red Shift in the Earth's Atmosphere
We
have explained that electromagnetic radiation having a length of
coherence much longer that the interatomic distance should not
produce bremsstrahlung. With the solar radiation the
critical pressure gives about 1015 at/cm3. This
same pressure exists in the Earth's atmosphere at 73 km above
the Earth's surface [43], and the column density above that altitude is 1.5×1019 at/cm2. Since
this is 700 times smaller than the column density above the
corresponding point on the Sun (having the same density), this
leads to a red shift that is 700 times smaller in the Earth's
atmosphere than one observed on the Sun. Consequently, no
observable red shift is expected to be detected in the Earth's
atmosphere.
V. Other Models
Let
us now consider the assumption that the CLV is a consequence of
a Doppler effect resulting from radial mass motion in the solar
photosphere or chromosphere, as reported by Finlay-Freundlich [11], Struve [13], and Snider [25]. It is clear that
the velocity of such a mass motion must be adjusted in order to
compensate exactly for the redshift on the center of the disk,
and also be adjusted exactly to the relativistic value on the
limb, since any radial motion has no effect on the limb as seen
from Earth. It is easily seen in Fig 1 that between 0.5
and 0.9 of the solar disk radius, mass motion leads to a CLV in
complete disagreement with experimental data. Again, in
Fig 2, above 0.900 these other models are in total disagreement
with the experimental data.
Finally,
let us compare the experimental results with the ones predicted
using the theory of microturbulence as calculated by Schatzman
and Magnan [18].
From [18, eq. (29) fig. 1] one can see that
the red shift varies almost linearly as a function of the
position on the solar radius. The same parameters used [18] give a redshift on the
limb of 0.35 km/s. Furthermore, the redshift at the center
of the disk is adjusted with a proper choice of the parameters
E/kT. The results are shown in Fig 1 and 2, and one can notice
again a serious discrepancy with the experimental data, as
stated by Schatzman and Magnan [18] themselves: "In fact, our theory predicts too
much red shifts". Other more recent works [26], [33], [20]
show that both horizontal and vertical motion in the solar
granulation can explain the red shift resulting from mass motion
inside granules, but does not lead to the observed CLV reported
by so many observers. Furthermore, Beckers and Nelson [30] report: "A
quantitative interpretation of the limb shift in terms of
our convection model leads, however, to conclusions which
are to some extent at variance with our present concept of
solar granulation."
The
difficulty of using the existing theories involving granules to
explain CLV has been described in more detail at the beginning
of this paper and can be summarized by the recent statement
(1984) of Balthasar [44]: "Up to now, no complete and satisfactory
explanation for the line asymmetries known since 1956 and
the limb effect known since 1907 exist."
Finally,
another comment must be added since the absorption lines are
relatively wide (several times wider than the redshift) and
asymmetric. Their relative displacement leading to CLV has
been accurately measured, but their absolute position within the
individual line profile is much more difficult to
establish. The difficulty of absolute measurements in the
presence of pressure shifts and convection might account for a
small constant shift across the solar disk. In these solar
measurements, the wavelength reference is the minimum [43] in the spectrum. It
is well known to spectroscopists that, due to line shapes and
pressure broadening, precise location of atomic and molecular
levels is not necessarily situated at the position of the
maximum absorption, especially when the profile is
asymmetric. The accurate difference in wavelength between
the actual position of an atomic level and the position of
maximum absorption is still an undetermined quantity in solar
lines.
At
the solar disk center, it is important to notice that Balthasar
[44] reports precise
measurements showing that observed wavelengths "depends
strongly on the formation depths of the lines: Lines formed
in higher layers show larger redshifts."
Balthaser [44] also
reports that lines formed in the highest layers "have
shifts of about the gravitational red shift" To
explain it more clearly, it is reported [45] that the difference between the wavelength of a given
absorption line of iron observed at the disk center and formed
in the highest layers of the solar chromosphere and the
laboratory wavelength measurement is exactly equal to the
gravitational red shift. Furthermore, it is also
suggested [44]
that the upward velocity of "the ascending matter is
decelerated". This effect explains the decreasing
blueshift of the radiation issued at an increasing altitude, as
observed experimentally by Crosswhite [45] and reported by Balthasar [44]. It is extremely interesting to observe that
relativistic corrections, combined with the upward velocity
reported [44], [45], lead to zero vertical
velocity in the "highest layers". At the solar disk
center, it can also be calculated that the Doppler blueshift
resulting from the upward velocity of the "lowers layers"
overcompensates for the redshift produced by the gas. We
see now that the systematic investigation of the depth
dependance of a lot of spectral lines done by Balthasar [44] was necessary for the
understanding of the problem. These conclusions are in
exellent agreement with the observations of the new red shift
theory presented above.
VI. Lines Profiles
As
stated previously [14], [15],
experimentally measured line profiles are modified and become
more asymmetric near the limb. This asymmetry has not been
clearly explained, as indicated by Higgs [14], [15] and
in more recent papers. In the case of red shifts due to
bremstrahlung on atoms, we will see that the same method used
for calculating the amount of gas in the solar chromosphere can
be used to determine the line profiles. It is clear that
the absorbing solar chromosphere has a non-negligible thickness,
and the medium producing the absorption is the same as the one
producing the red shift. Absorption lines produced in the
gas in the upper part of the solar chromosphere will not be red
shifted significantly since the photons do not go through enough
gas before reaching the Earth. On the other hand, gas at a
lower altitude will produce specific absorption lines that will
be red shifted due to the presence of gas at a higher solar
altitude before reaching the Earth. The final result is
that the absorption features will appear at slightly different
wavelengths as seen from Earth, depending on the altitude or the
altitude range where the absorption takes place in the solar
atmosphere. A larger altitude range will produce a
broadening of the absorption lines. Finally, if the
absorption coefficient is not constant, as is the case when the
FeI atoms have different temperatures and densities, the widened
lines become asymmetric. This is precisely what has been
observed experimentally [15].
Let
us assume that the line profile within a layer has a Gaussian
distribution. The absorption profile coming from the
lowest layer (#1) is red shifted and added to the profile
produced by the next layer (#2), and so on. One sees that
the profile from layer (#1) is more redshifted when reaching the
Earth than the profile of layer #2. A calculation using
40-Gaussian functions with linearly decreasing amplitudes has
been used as an example in order to illustrate the contribution
of uniformly spaced red shifts (originating from layers giving
different absorption). It is found that this leads to a width
three times as wide as the width of the Gaussian function (at
half height). The result of these calculations shows that
the calculated profile, shown as "B" in Fig. 3, is similar to a
typical asymmetric profile :A" (Fig. 3) observed by Higgs [14, fig. 4] . For a larger column
density, the calculated red shift is larger with respect to the
width of the lines and has a larger asymmetry, as observed
experimentally [14],
[15]. Finally, it
can be shown that the asymmetry can be different and even
reversed if the absorption takes place in different
conditions. One must conclude that the red shift resulting
from bremsstrahlung, as predicted [3], [5],
leads naturally to asymmetries of the type observed in solar
spectra.
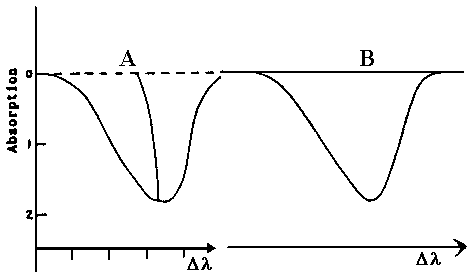
Figure 3
Curve A is the line profile reported by
Higgs (ref. [14])
(experimental)
Curve B is a typical line profile according to
this work (theory)
VII.
Further Observations
Apart
from the fact that the basic theory described by Marmet [3], [5]explains for the first time the absolute amplitude and
the shape of the CLV of spectral lines across the solar disk
without and ad hoc hypothesis or adjustable parameters, several
observations that have received no clear explanation previously
support the theory applied here. Let us cite two of them:
1)
Very recently, Balthasar [44] stated: "A missing limb effect for several
lines formed in very high layers was reported by Schröter [46]*, Appenzeller and
Schröter [37],
Roca-Cortes el al. [47]*."
Such a result, which has also been observed by Snider [25] several years ago, is
deduced naturally from the theory put forward here, since no red
shift can be produced from the highest layers, because there is
insufficient column density between the Sun and the Earth to
produce a measurable red shift.
2)
Balthasar [44] also
reports that "a stronger limb effect for the higher formed
line at 5250 Å than for the higher line at 5576 Å"
has been found by Bruning [36]. This line-dependent variation of red shift is
easy to explain with our present model. The larger limb
effect of line 5250 Å is due to the fact that the radiation has
to go through a larger amount of (red shifting) gas before
reaching the observer on Earth.
Thus,
the theory which takes bremsstrahlung into account explains
precisely the absolute amplitude of the CLV, its variation as a
function of its position on the disk and near the limb, and even
the change in lineshapes especially near the limb without having
to introduce any ad hoc theory or parameters.
Acknowledgment
The
author wished to acknowledge fruitful discussions with Dr. G.
Herzberg and Dr. P. Feldman of the Herzberg Institute of
Astrophysics, Prof. P. Marchand of Laval University, Dr. L.
Higgs of the Division of Radio Astronomical Observatory in
Pentincton, B.C. Can., Dr. J. W. Kierein of the Aerospace
Systems Division, Dr. M. Proulx and Dr. P. Plessis of the
National Research Council of Canada, Ottawa, and L. Marmet of
the University of Toronto.
References
[1] A. L. Peratt "Dean of the
Plasma Dissidents" Natural Sciences, The World and I. pp.
190-197, May 1988.
[2] G. Reber "Intergalactic
Plasma" IEEE Trans. Plasma Sci., Vol. PS-14, pp. 678-682, Dec.
1986.
[3] P. Marmet, "A New Non-Doppler Redshift"
département de physique, Université Laval, Québec, Canada, 1981,
p. 64.
[4] P. Marmet, presented at the
Symp. Fundamentals of Collision Processes in the Presence of
Intense Laser Fields, St. Francis Xavier University,
Antigonish, N.S., Canada, Aug, 12-16, 1985.
[5] P. Marmet, "A New Non-Doppler Redshift"
Physics Essays, Vol.
1 pp. 24-32, 1988.
[6] J. Halm, Über eine bisher
unbekannte verschiebung der Fraunhoferschen linien des
sonnenspectrums, Astron, Nachr., Vol. 173 pp. 273-288, 1907.
[7] W. S. Adams, "An
Investigation of the Displacements of the Spectrum Lines at the
Sun's Limb", Astrophys. J., Vol 31, pp. 30-61, 1910.
[8] M. G. Adam, "Interferometric
Measurements of Solar wave-lengths and an Investigation of the
Einstein Gravitational Displacement", Mon. Notic. Roy. Astron.
Soc. Vol. 108. pp. 446-464, 1948.
[9] M. G. Adam, "Interferometric
Measurements of Wave-lengths", Mon. Notic. Roy. Astron. Soc.
Vol. 115, pp. 405-421, 1955.
[10] M. G. Adam, "A New
Determination of the Center-to-limb change in the Solar
wavelengths. "Mon. Notic. Roy. Astron. Soc. Vol. 119. pp.
460-474, 1959.
[11] E. Finlay-Freundlich, "Red
Shift in the Spectra of Celestial Bodies", Phil. Mag. Vol. 7 pp.
303-319, 1954.
[12] E. H. Schröter, "Zur
deutung der rotverschiebung und Mitte-Rand-variation der
Fraunhoferlinien bei berücksichtigung der temperaturschwankungen
der sonnenatmosphäre" Z. Astrophys. Vol. 41, pp. 141-181,
1957.
[13] O. Struve, Elementary
Astronomy, New York, Oxford Univ. Press. pp. 364, 1959.
[14] L. A. Higgs, " The solar
Redshift ", Mon. Notic. Roy. Astron. Soc. Vol. 121, pp. 421-435,
1960.
[15] L. A. Higgs, Asymmetry of
Solar Line Profiles", Mon. Notic. Roy. Astron. Soc. Vol. 124,
pp. 51-59, 1962.
[16] R. Kh. Salman-Zade,
Astron. Zh. Vol. 46. pp. 589-599, 1969. (translation: "Limb
Effect of the Fraunhofer Lines in the Solar Spectrum" Sov.
Astron. AJ. Vol. 13, pp. 466-472, 1969).
[17] J. L. Snider, "Atomic Beam
Study of the 7699 Å Potassium Line and the Gravitational Red
Shift" Sol. Phys. Vol. 12. pp. 352-369, 1970.
[18] E. Schatzman and C.
Magnan, "Shifts and Asymmetries of Lines Formed in a Thermally
Driven Turbulent Medium, Astron. Astrophys. Vol. 38. pp.
373-380. 1975.
[19] J. C. Pecker, "Décalage
vers le rouge et expansion de l'univers." Paris: Éditions de
CNRS, p. 619, 1977.
[20] J. M. Beckers and L. E.
Cram, "Use of the Solar Limb Effect to test Photon Decay and
Cosmological Red Shift Theories". Nature, Vol. 280, pp. 255-256,
1979.
[21] H. J. Reboul, "Untrivial
Redshifts: A Bibliographical Catalogue". Astron. Astrophys.
Suppl. Vol. 45, pp. 129-144, 1981.
[22] R. Howard, J. E. Boyden
and B. J. Labonte, "Solar Rotation Measurements at Mount
Wilson". Sol. Phys. Vol. 66. pp. 167-185. 1980.
[23] D. Dravins, "Photospheric
Spectrum Line Asymmetries and Wavelengths Shifts" Ann.
Astron. Astrophys. Vol. 20, pp. 61-89, 1982.
[24] J. Evershed and T. Royds,
"Report of the Kodaikanal Observatory", Kodaikanal Obs.
Bull. Vol. 3, pp. 145-156, 1916.
[25] J. L. Snider, "New
Measurement of the Solar Gravitational Redshift". Phys. Rev.
Lett. Vol. 28, pp. 853-856, 1972.
[26] F. Cavallini, G.
Ceppatelli and A. Righini, "Asymmetry and shift of Three
FeI Photoscopic Lines in Solar Active Regions" Astron.
Astrophys. Vol. 143, pp. 116-121, 1985.
[27] E. A. Gurtovenko, R. I.
Kostic, T. V. Orlova, V. I. Troyan and G. L. Fedorchenko,
"Profiles of Selected Fraunhofer Lines for Different
Center-to-Limb Positions at the Solar Disk". Kiev, Naukova,
Dunka, pp. 224, 1975.
[28] M. G. Adam, P. A. Ibbetson
and A. D. Petford, "The Solar Limb Effect: Observation of Line
Contours and Line Shifts". Mon. Notic. Roy. Astron. Soc. Vol.
177.pp. 687-708, 1976.
[29] P. N. Brandt and E. H.
Schröter, "On the Center-to-limb Variation and Latitude
Dependence on the Asymmetry and Wavelength Shift of the
Solar Line l5576." Sol. Phys. Vol. 79. pp. 3-18. 1982.
[30] J. M. Beckers and G. D.
Nelson, "Some Comments on the Limb Shift of Solar Lines".
Sol. Phys. Vol. 58. pp. 243-261, 1978.
[31] M. Kaisig, and C. J.
Durrant, "The Asymmetry of Photospheric Absorption Lines".
Astron. Astrophys. Vol. 116. pp. 332-340, 1982.
[32] J. W. Brault, "The
Gravitational Red Shift in the Solar Spectrum" Ph. D.
dissertation, Princeton Univ. Princeton. N. J. p. 87, 1962.
[33] F. Cavallini, G.
Ceppatelli and A. Righini, "Meridional and Equatorial
Center-to-limb Variation of the Asymmetry and shifts of Three
FeI Solar Photospheric Lines around 6300 Å". Astron.
Astrophys. Preprint 7, 1985.
[34] S. L. Keil, "The Structure
of Solar Granulation 1: Observation of the Spatial and Temporal
Behavior of Vertical Motions". Astrophys. J. Vol. 237. pp.
1024-1034, 1980.
[35] B. J. Labonte and R.
Howard, "Solar Rotation Measurements at Mount Wilson: III
Meridional Flow and Limbshift" Sol. Phys. Vol. 80, pp.
361-372, 1982.
[36] D. H. Bruning
"Empirical Limb Effect Curves for the FeI Lines l5250 and
l5576". Sol. Phys. Vol. 71. pp. 233-236, 1981.
[37] I. Appenzeller and E. H.
Schröter, "Center-to-limb Variations of the Intensity and the
Wavelength of Several Fraunhofer Lines along the Sun's Polar and
Equatorial Diameter". Astrophys. J. Vol. 147, pp. 1100-1105,
1967.
[38] T. L. Duvall Jr., "Large
Scale Solar Velocity Fields". Ph. D. dissertation, Stanford
Univ. Palo Alto CA, 1977
[39] T. L. Duvall Jr., "Large
Scale Solar Velocity Fields". Sol Phys. Vol. 63. pp. 3-15,
1979.
[40] J. W. Kierein and B. M.
Sharp, Compton effect Interpretation of Solar Red Shifts", Sol.
Phys. Vol. 3, pp. 450-453, 1968.
[41] H. A. Bethe and E. E.
Salpeter, "Quantum Mechanics of One and Two Electron Atoms".
Berlin Göttinger, Heidelberg: Springer-Verlag, pp. 369, 1957.
[42] J. M. Jauch and F.
Rohrlich, "The Theory of Photons and Electrons" New York,
Berlin, Heidelberg: Springer-Verlag, p. 364, 1980.
[43] C. W. Allen,
"Astrophysical Quantities", 3rd Edition, London: Athlone Press,
Univ. of London, 1973.
[44] H. Balthasar, "Asymmetries
and Wavelengths of Solar Spectral Lines and the Solar Rotation
Determined from Fourier Transform Spectra", Sol. Phys.
Vol. 93. pp. 219-241, 1984.
[45] H. M. Crosswhite,
"The Iron-Neon Hollow Cathode Spectrum". J. Res. Nat. Bur.
Stand. Sect. A. Vol. 79. p. 17. 1975.
[46] E. H. Schröter,
"Rotverschiebung und 'Limb-Effekt' im Sonnenspektrum" Mitt.
Astrophys. Obs. Postdam Nr. Vol. 83. No:4, pp. 69-75, 1959
[47] T. Roca-Cortes, M.
Vásquez, and H. Wöhl, "Space and Time Variations of K1 7699
Solar Line Profile". Sol. Phys. Vol. 88, pp. 1-8, 1983.