11.1 - Introduction.
In this
chapter, we will give a physical description of the absolute
changes that happen inside an hydrogen atom when it is accelerated
to a high velocity. We have seen that this acceleration produces
an increase of the electron mass and in the Bohr radius. We also
notice from chapter three that the principle of mass-energy
conservation is respected inside the hydrogen atom without having
to involve any change of electric charge when the hydrogen atom is
brought to high velocity. We will now show how the absolute
parameters of the hydrogen atom change when it acquires kinetic
energy. We present some considerations to the problem of internal
potentials inside the nucleus of atoms. Finally, we will see how
the nature of the interactions taking place inside nuclei can be
predicted using these considerations.
11.2 - Transformations
inside Fast Moving Atoms.
We have
seen in equation 3.4 that when the velocity of the hydrogen atom
increases, the absolute value of the Bohr radius a
increases according to:
| av[rest] = gao[rest] |
11.1 |
where ao[rest]
is
the
Bohr
radius at rest in rest units, and av[rest] is
the Bohr radius at velocity v, also in rest units. The units in
this chapter will always be rest units so that we will drop the
index [rest]. Let us use a numerical example to illustrate some of
the absolute changes taking place inside atoms accelerated to a
high velocity. When an hydrogen atom moves at v = 0.866c, then g = 2. We will consider the hydrogen atom
in its ground state but one can see that the transformations can
be applied, in a similar way for any excited state. From equation
11.1, when v = 0.866c, we have:
We know
from equation 2.23 that the electron mass increases when it moves
faster:
Therefore
the absolute electron mass of a hydrogen atom moving at velocity v
= 0.866c becomes:
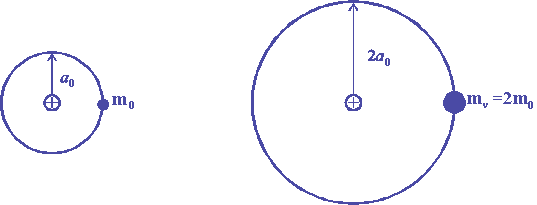
Figure 11.1
Figure
11.1, illustrates the simultaneous increase of the Bohr radius
and of the electron mass when g = 2.
Let us examine how these results are compatible with the Bohr
model, the de Broglie wavelength of particles and quantum
mechanics.
11.3 - Electric
Potentials.
Let us
examine first the compatibility between the description given
above with the laws regulating the electron and the proton in
the hydrogen atom. We recall that when an atom is accelerated to
a high velocity, the electric charges and the absolute electric
field around those charges do not have to change in order to
remain compatible with the principle of mass-energy
conservation. The electric energy Eo of the electron
in the electric field of the proton is:
 |
11.5 |
where k
is the Coulomb constant, e+ and e- are the electric charges of the
proton and the electron and ao is the average
distance between the electron and the proton which corresponds to
the Bohr radius. Putting equation 11.2 in 11.5, we find that the
internal electric energy Ev inside the moving hydrogen
atom is:
 |
11.6 |
Since the
compatibility between observations and mass-energy conservation
has been obtained without modifying the electric charge when
a particle is accelerated, we can write:
| e-o
[rest] = e-v
[rest] |
11.7 |
The
problem of an electric charge moving in a variable gravitational
potential of the Sun, has been considered previously (in the case
of the Mercury problem) in chapter one, and will be discussed
later in detail in a separate paper. This will not be
discussed here.
In
the case of kinetic energy, in order to be able to establish
comparisons, all parameters are calculated using rest units.
According to the Bohr model of the atom, when the electron of the
hydrogen atom moves in an electric field (i.e. the field of the
proton), one must have an equilibrium between the attracting
electric force and the centrifugal force. The electric and
the centrifugal forces are defined as:
 |
11.8 |
In
order to be compatible with Newton physics, these forces must be
equal. We have:
 |
11.9 |
Equations
11.8 and 11.9 give:
 |
11.10 |
For the
hydrogen atom at rest, the distance a is equal to the Bohr
radius ao. We have:
 |
11.11 |
For the
hydrogen atom at velocity v, a = av and
we have:
 |
11.12 |
We recall
that the parameters 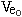 and
and 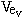 here are the electron velocities with respect
to the proton. The velocity of the hydrogen atom is expressed
using g (and v without a subscript).
Using equations 11.2 and 11.4 in equations 11.11 and 11.12 gives
(for g = 2):
here are the electron velocities with respect
to the proton. The velocity of the hydrogen atom is expressed
using g (and v without a subscript).
Using equations 11.2 and 11.4 in equations 11.11 and 11.12 gives
(for g = 2):
 |
11.13 |
where 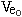 is the electron velocity with respect to the
proton when the hydrogen atom is at rest and
is the electron velocity with respect to the
proton when the hydrogen atom is at rest and 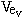 is the electron velocity with respect to the
proton when the hydrogen atom has the velocity v = 0.866c. From
equation 11.13, the electron velocity (with respect to the
nucleus) is reduced by half when the hydrogen atom is accelerated
to a velocity v = 0.866c.
is the electron velocity with respect to the
proton when the hydrogen atom has the velocity v = 0.866c. From
equation 11.13, the electron velocity (with respect to the
nucleus) is reduced by half when the hydrogen atom is accelerated
to a velocity v = 0.866c.
In order
to be compatible with the Bohr equation and quantum mechanics, the
length of the circumference of the orbit of an electron around a
proton must be equal to an integer number of the wavelength of the
electron. In the case of the hydrogen ground state, the electron
wavelength must be equal to the length of one circular orbit. The
de Broglie wavelength l is given by:
 |
11.14 |
Putting
equations 2.22, 2.23 and 11.13 in 11.14, the wavelength 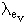 in the moving frame is :
in the moving frame is :
 |
11.15 |
Equation
11.15 shows that the electron wavelength
orbiting the moving atom is twice as long as the electron
wavelength of the atom at rest. Consequently, the radius of the
electron orbit is twice as large, when the atom moves at
velocity v=0.866c. This satisfies perfectly the conditions
required above in equation 11.2 when the requirements of quantum
mechanics are applied.
This satisfies
the wave condition of the constructive interference of the
electron wave after each translation since the radius of the orbit
(therefore its circumference) of the moving atom is twice as large
as the radius for the atom at rest as illustrated on figure 11.1.
Furthermore, when all these fundamental conditions are perfectly
satisfied, the frequency of emission of light between electronic
transitions is reduced by two, since the energy between the states
is reduced by two when the atom is moving, exactly as observed
experimentally from the red shift of spectral lines and from the
slowdown of moving atomic clocks. It is this absolute reduction of
frequency of a moving clock located in a moving frame that has
been erroneously interpreted by Einstein as time dilation.
We must
then conclude that the predicted absolute change of parameters
inside a moving frame, resulting from mass-energy conservation is
coherent inside moving atoms. We must also note that all the
transformations given above are in perfect agreement with constant
absolute electric charges in all frames when
kinetic energy is added to atoms. (see
equations 11.7 and 11.8). We recall that this absolute electric
field is similar to the absolute gravitational field shown in
chapters four and five. This agreement proves the invariability of
the electric forces as well as the quadratic decrease of the
electric field around charges in all frames. This result
agrees perfectly with the well observed experiment showing that
electric charges moving at high velocity in a magnetic field
travel along a larger radius of curvature corresponding to a
different value of e/m. This smaller ratio of electric charge over
electron mass is due to an increase of mass (due to kinetic energy) while there
is no change of electric charge. Therefore,
experimental results show that the ratio of the electric charge
over the mass of electrons (e/m) is different in fast moving
particles.
11.4 - Sommerfeld Fine
Structure.
The
prediction of the advance of the perihelion of Mercury seen in
chapter five is not the sole example of the success of the
principle of mass-energy conservation and classical mechanics.
There is also a well documented example in atomic and molecular
physics in which it is clearly observed that the principle of
mass-energy conservation influences the electronic structure
inside atoms. There are many similarities between Mercury moving
inside the gravitational field of the Sun and the electrons of
atoms orbiting inside the electric potential of the proton.
However, an important difference is that the electron mass is
not concentrated into a relatively small location with respect
to the size of the atom contrary to the case of Mercury and the
Sun.
Since
electrons exist as waves, the electric potential between the
electron cloud and the proton can be calculated using the wave
distribution given in quantum
mechanics. This leads to the same average energy and distance ao
that we would find if all the electron was concentrated at a
distance equal to the Bohr radius from the proton. Consequently,
one can calculate the potential of that electron cloud using
quantum mechanics, as if it were located at a distance from the
proton, equal to the Bohr radius. That electron cloud can either
oscillate through the proton if the angular momentum is zero or
around it, if the angular momentum is not zero.
When
the electron cloud is trapped into the electric field of a
proton, an hydrogen atom is formed. During its formation, energy
is given up as emitted radiation. This is similar to the energy
that Mercury must release when it is trapped into the Sun's
gravitational potential. The electron cloud can be distributed
according to many configurations having different energies
corresponding to different quantum states. Consequently, during
the formation of each of those states, the electron loses mass
the same way Mercury does when it is trapped in the Sun's
gravitational potential.
Let us
use the Bohr model in which an electron moves on an orbit around
the nucleus. We know that the Rydberg states of hydrogen
correspond to electrons traveling on an orbit whose
circumference is exactly equal to an integer number of the
wavelength of the electron. Then, there is a constructive
interference of the electron wave when moving to the next orbit
around the nucleus. The number of wavelengths forming the orbit
is equal to the principal quantum number. This model is
compatible with the energies calculated by quantum mechanics.
Experimentally, after the Rydberg states were measured, it was
noticed that the transitions between these states are not as
simple as originally expected. It was discovered that the
transitions between each pair of states are generally made of
several very close spectral lines. Sommerfeld carried out
calculations using general relativity and he discovered that
instead of simple transitions between quantum states, there
should be multiple transitions due to the fine structure.
Due to
the change of electron mass as a function of its distance from
the proton, the wavelength of the electron changes.
Consequently, the radius of the orbit changes because it is
necessary to have an integer number of wavelengths in a
circumference. Due to that change of the distance from the
proton, the electrostatic potential changes so that the electron
energy becomes different. Consequently, the force
(not the field) between the electron and the proton does not
follow exactly a quadratic function. Therefore the electron
orbit around the proton precesses as in the case of Mercury
around the Sun as given in equation 5.52. Due to this
precession, the transitions between different quantum states
have slightly different energies depending on the relative
direction of the velocity of the electron around the nucleus
involved in the quantum transition.
Experimentally, the fine structure is well known. The Sommerfeld
fine structure constant is equal to:
 |
11.16 |
where h
is the Planck parameter.
This fine
structure term is observed between all quantum states as long as
transitions are allowed by the selection rules. Sommerfeld's fine
structure is explained in many textbooks [1]. It is often
illustrated by precessing ellipses forming rosettes identical to
the path of Mercury on figure 6.2.
The
Sommerfeld fine structure constant can be explained more
accurately using the principle of mass-energy conservation as done
in the case of the orbit of Mercury. However, this is beyond the
scope of this book. We will limit our explanations to this
qualitative description. We understand now that the fine structure
inside atoms is due to the principle of mass-energy conservation.
Of course, Sommerfeld's calculations do not lead to a complete
agreement in the case of an electron, because one must consider
the electron spin. However, this last correction is irrelevant in
the case of Mercury.
11.5 - Atomic Structure
inside Free Falling Atoms.
Let us
study a hydrogen atom falling freely in a gravitational field.
We can assume that the atom was initially located in outer space
before it slowly started to drift and accelerate gradually
toward the Sun. Then, gradually, the hydrogen atom acquires a
high velocity. An observer accompanying the falling mass would
not feel any internal acceleration. We will now
calculate the absolute rate of the falling clock.
Let us
examine this problem separating mathematically the two
components of energy acting on the falling mass. With respect to
a rest frame in outer space, the speeding hydrogen atom is now
at a location where there exists a gravitational potential. We
have seen that to calculate the exact mass of the particle, this
potential must be taken into account. Furthermore, the falling
hydrogen has acquired a velocity which must also be taken into
account.
We have
seen in equation 1.22 that the gravitational potential, where
the atom is now located, is such that the mass of the particle
has decreased and is now different from its mass in outer space.
We also know that the kinetic energy increases the mass of the
particle by an amount, which must be equal to the mass lost due
to the potential energy.
This
can be easily calculated and we see that the decrease of mass
due to the gravitational potential compensates exactly the
increase of mass due to kinetic energy. Consequently, the
absolute mass of the particle (proton and electron) does not
change while it is falling.
11.6 - High Potentials
and Higher Order Terms.
Contrary to Einstein, in this book we have not arbitrarily
postulated that physical quantities are invariant in all frames.
We have used only the principle of mass-energy conservation.
However, we have found that when we consider the zero and first
orders of v/c (or the gravitational potential), the physical
laws appear (almost) invariant in all frames as arbitrarily
assumed by Einstein. In that particular case, the physical
consequences are almost all identical to what Einstein found
with his arbitrary postulate. However, our results are obtained
using solely the principle of mass-energy conservation. The
physical laws derived from the use of the first order of v/c are
invariant, up to the point we reach higher order terms in (v/c)2 and other still higher terms (however small) that
have been neglected.
One
could repeat all the above calculations without neglecting the
higher order terms. Then, one could have an exact answer to the
problem of extreme energies. We can foresee that if we dealt
with physical phenomena in which the higher terms were not
negligible (correction due to velocity), the physical laws
observed might be slightly different. Within those physical
limiting conditions, at high energy, the behavior of matter
would not correspond to the description we are used to see in a
rest frame and in a frame in which the ratio v/c is not too
high.
We have
to realize that the experimental conditions that correspond to
such high energies are quite common in physics. It is clear that
when the nucleus of an atom emits particles having energies of
millions of electron volts, the second and third order terms of
the potential involved are not negligible. Consequently, we
expect that the internal phenomena taking place in the nucleus
of atoms at such high potential taking into account the higher
order terms lead to physics we are not accustomed to see. It is
for that reason that nuclear forces are not familiar to us and
to classical mechanics. We believe that the principle of
mass-energy conservation is one of the ultimate principles in
physics that possesses the wonderful power of informing us, in a
logical way, on the correct physical nature of the forces
involved in nuclear and particle physics. Mass-energy
conservation is relevant everywhere in physics
and can be applied everywhere in nature, especially when
enormous potentials are involved as in the nucleus of atoms and
at the center of the stars.
A
general study of physics in which the principle of mass-energy
conservation is fully applied is beyond the scope of this book.
However, we are convinced that a physical and realistic
description of our physical world can be logically achieved
without having to involve the non-realistic, the
non-conservation of mass-energy and the contradictory hypotheses
used in modern physics [2].
11.7 - References.
[1] H. Semat, Introduction
to
Atomic
and
Nuclear Physics, Holt, Rinehart and Winston, Forth
edition, P. 245, 1962.
[2] P. Marmet,
Les …ditions du
Nordir, c/o R. Yergeau, 165 Waller Street, Simard Hall,
Ottawa, On. Canada K1N 6N5, 144p. 1993.
11.8 - Symbols and
Variables.
| ao |
Bohr radius of the atom at rest |
| av |
Bohr radius of the moving atom |
| Eo |
Electric energy of the atom at rest |
| Ev |
Electric energy of the moving atom |
| lo |
de Broglie wavelength of the atom at
rest |
| lv |
de Broglie wavelength of the moving atom |
| mo |
mass of the atom at rest |
| mv |
mass of the moving atom |
| vo |
velocity of the electron relative to the
proton of the atom at rest |
| vv |
velocity of the electron relative to the
proton of the moving atom |
<><><><><><><><><><><><>
Chapter10
Contents
Chapter 12
Return To: List of Papers on the Web
Where to get a Hard Copy of this Book
 Einstein's
Theory
of
Relativity
Einstein's
Theory
of
Relativity
Einstein's Theory of Relativity






