Einstein's
Theory of Relativity
Einstein's
Theory of Relativity
versus
Classical Mechanics
by Paul Marmet
Chapter Twelve
On the Formation of Pseudo Black Holes.
12.1 - Formation of a
Protostar.
In this
chapter, we will consider what happens to a large volume of gas
when taking into account the gravitational field of each
individual atom. As an example, we use a nebula containing N atoms
of hydrogen. Due to Newton's universal law of gravitation, all
these individual electrically neutral particles attract each
other. Consequently, each atom slowly drifts toward the center of
the system. The gas becomes more and more compact as a function of
time and the nebula occupies a gradually smaller volume of space.
During
the collapse of the nebula, the velocity of the particles
increases due to the increasing gravitational potential created by
the increasing concentration of matter. The density and the
velocity of individual atoms augment so that the temperature
increases while the radius of the volume of gas decreases.
Consequently, the gas becomes very hot. These high temperature and
density produce a high pressure that reduces the collapsing rate.
Due to
Planck's law of radiation, the gas emits its thermal energy as
electromagnetic radiation to outer space. This phenomenon causes a
reduction of the internal temperature and pressure so that the
star can progress with further shrinking. These two processes go
on simultaneously as long as the star has enough mass to produce a
gravitational force sufficiently large to produce further
shrinking. The shrinking rate of the star depends on the rate of
emission of energy of the star through radiation. An equilibrium
exists between the atomic, molecular or nuclear forces which
provoke emission of radiation at high temperature and the
gravitational forces.
In the
above qualitative description, we consider that the number N of
hydrogen atoms does not change during the contraction of the
nebula into a star. However, a large amount of energy has to be
emitted from the star through radiation in order to get rid of the
thermal energy. One must take into account the principle of
mass-energy conservation requiring the mass of the star to
decrease because of the radiation emitted due to Planck's law of
radiation. 12.2
- Mass-Energy Conservation in Clusters of Atoms.
In order
to satisfy the principle of mass-energy conservation, let us
calculate quantitatively the amount of energy that must be emitted
from the protostar when it is transformed from a nebula to a high
density star. Let us start with an initial very large diffuse
nebula. We will calculate the change of gravitational energy when
the nebula takes the shape of a hollow sphere of radius R.
Let us
calculate the gravitational energy when N hydrogen atoms coming
from the nebula have all reached the distance R from the center of
mass. When the first atoms reach that distance, the sphere is
infinitely thin. The potential energy met by each new individual
atom increases with the number of atoms (mass) that has already
reached the distance R. This process goes on until all atoms have
formed a sphere of radius R. We have then a spherical protostar.
In order
to calculate the total internal gravitational potential of such a
star, let us use the building up principle and accumulate
individual hydrogen atoms, one by one. In the case of the Sun, the
number of hydrogen atoms needed is about 1.2×1057. Each
individual atom is systematically brought from a large distance in
outer space to the location at a distance R from the center of the
stellar mass being formed. We consider the approximation of a
hollow sphere because we want to keep the potential constant
inside the star.
The very
first step in the formation of the star is to bring two hydrogen
atoms together at a distance R. At that distance, the atoms have
acquired gravitational energy E{1} due to the gravitational
potential between them. This gravitational energy is given by:
 |
12.1 |
where mH
is the mass of the hydrogen atom. The two particles remain trapped
at a distance R in this gravitational potential if the amount of
electromagnetic energy emitted is equal to E{1}. The equivalent
loss of mass to stabilize this interaction is equal to:
 |
12.2 |
Therefore, after stabilization by the emission of radiation, using
equations 12.1 and 12.2, we find that the remaining mass M{1} of
the pair of hydrogen atoms (at distance R) is:
 |
12.3 |
After the
formation of the first pair of hydrogen atoms, let a new hydrogen
atom fall (at a distance R) into the gravitational field produced
by the new pair. The new hydrogen atom of mass mH interacts at a distance R from the pair of mass M{1}
previously formed and described in equation 12.3. Using Newton's
law, the gravitational energy between the pair of hydrogen atoms
with mass M{1} and the individual hydrogen mH atom is:
 |
12.4 |
We might
want to explain how the new hydrogen atom can be at an effective
distance R from the previous pair of atoms. The distance R
mentioned here means that the new atom is located at a distance R
from the previously formed pair so that the gravitational
potential between the new atom and the pair is equivalent to the
potential that would exist if the previously formed pair of atoms
were close together and the new atom were at a distance R from the
pair. This description is supported mathematically by a theorem
(used in electrostatics) which shows that the potential created at
the surface of a spherical distribution of charges is the same as
if all the charges were located at the center of the sphere. We
will apply this same theorem here for the case of the
gravitational potential of particles approaching the spherical
distribution of matter forming the star.
In
equation 12.4, the mass DM{2} lost
after emitting thermal energy is:
 |
12.5 |
The total
mass M{2} of the three hydrogen atoms is then:
| M{2} = M{1} + mH - DM{2} |
12.6 |
 |
12.7 |
Equations 12.7, 12.3 and 12.4 give:
 |
12.8 |
Of
course, when a star is formed, the energy does not have to be
emitted immediately after the addition of each individual atom.
When particles are brought together, they form a hot gas in
their gravitational potential which cools down later by the
emission of radiation. There is no difference of energy if the
radiation is emitted immediately or later.
Repeating the operation and adding a fourth hydrogen atom to the
set of three atoms gives:
 |
12.9 |
Equations 12.8 and 12.9 give:
 |
12.10 |
Adding
another hydrogen atom to the growing mass gives:
 |
12.11 |
Equations 12.10 and 12.11 give:
 |
12.12 |
Let us
define:
 |
12.13 |
Then:
| M{4} = 5mH -
10mH2 Z +
10mH3 Z2 - 5mH4 Z3 + mH5 Z4 |
12.14 |
Adding
another hydrogen atom gives:
| M{5} = 6mH -
15mH2 Z +
20mH3 Z2 - 15mH4 Z3 + 6mH5 Z4 - mH6 Z5 |
12.15 |
The
seventh hydrogen atom gives:
| M{6} = 7mH -
21mH2 Z +
35mH3 Z2 - 35mH4 Z3 + 21mH5 Z4 - 7mH6 Z5 + mH7 Z6 |
12.16 |
Going
on with more individual atoms but limiting our calculations to
the fourth power of mH gives:
| M{7} = 8mH -
28mH2 Z +
56mH3 Z2 - 70mH4 Z3 |
12.17 |
| M{8} = 9mH - 36mH2 Z + 84mH3 Z2 - 126mH4 Z3 |
12.18 |
| M{9} = 10mH
- 45mH2 Z +
120mH3 Z2 - 210mH4 Z3 |
12.19 |
| M{10} = 11mH
- 55mH2 Z +
165mH3 Z2 - 330mH4 Z3 |
12.20 |
| M{11} = 12mH
- 66mH2 Z +
220mH3 Z2 - 495mH4 Z3. |
12.21 |
The
coefficients of the equations above can be generalized to give:
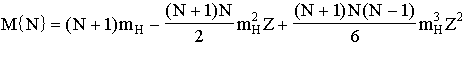
 |
12.22 |
For a star
like the Sun, the value of N is about 1057. Then for
N>>1 equation 12.22 gives:
 |
12.23 |
which
is identical to:
|

|
12.24 |
 |
12.25 |
Let us
define:
Equation 12.25 becomes:
 |
12.27 |
This
can be written (N is so large that it can be approximated to ¥ ):
 |
12.28 |
We
recall that Y = NmH is the
total mass of the nebula that formed the star. This would be the
mass of the star if there were no energy (mass) lost through
radiation during the formation. M{N} is the final mass of the
star made of N hydrogen atoms after taking into account the
thermal energy emitted as explained above.
12.3 - Mass of a Star
versus the Amount of Matter Used for Its Formation.
Equation 12.28 gives the mass
of the star as a function of the amount of matter Y used to form
it. Of course, when a larger amount of matter falls into the
gravitational potential, thermal energy is emitted and the
amount of mass lost into radiation increases. In these
calculations, the value of Z (from equation 12.13) is kept
constant when we study a star having a fixed radius R. Figure
12.1 shows the final mass of the star (after temperature
stabilization) as a function of the total mass falling on it,
using Z = 1 in equation 12.28.
We see
on figure 12.1 and from equation 12.28, that for a very small
amount of hydrogen atoms, the total mass of the star is almost
the same as the mass of the atoms used before the formation.
However, when the number of atoms accumulated in the star
becomes larger, the gravitational potential acting on each newly
added hydrogen atom becomes increasingly important.
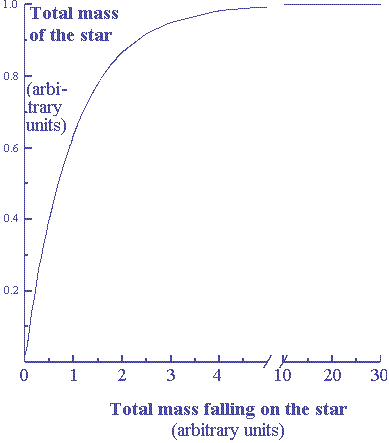
Figure 12.1
More
energy is lost in thermal radiation after each new hydrogen atom
is added. Consequently, an increasing fraction of the new mass
is lost when the star becomes more massive.
Here is
a numerical example obtained from equation 12.28. When the total
input of mass from the nebula is 0.01 (YZ = 0.01), independently
of the value of Z, about 99.5% of that mass remains in the star.
For one unit (YZ = 1.0) of input mass, the final mass is 63% of
the initial matter. When the input mass is ten units (YZ =
10.0), only 0.005% of the new mass is added to the star.
Finally, when the amount of matter given by the nebula to form
the star becomes much larger, the new mass added to the star
becomes almost completely transformed into energy due to the
gigantic gravitational potential. Therefore the mass of the star
no longer increases when the value of YZ gets very large (as
shown on figure 12.1).
12.4 - Mass of a Star
versus its Radius.
Within
the limits explained above, let us now consider a different way
to build a star. Instead of increasing the amount of matter from
outer space while forming the star at a constant radius, we use
a constant number of hydrogen atoms from the nebula but all
matter is contracted into a star of radius R.
When
the star is initially very big, the gravitational potential at
its surface is negligible. A very large star appears almost like
a concentrated nebula without an intense gravitational
potential. However, when the radius gets smaller, the high
density star generates a much higher gravitational potential so
the increase of temperature generates radiation which causes a
loss of mass-energy of the shrinking star. Using equation 12.28,
we can calculate the radius of the star formed from a
contracting nebula containing a constant number of atoms of
matter. During the decrease of the radius, the star is
maintained at a relatively low temperature (of a few tens of
thousand degrees), due to Planck's emission of radiation.
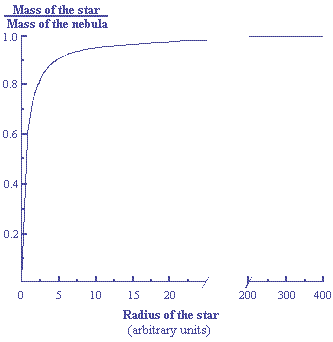
Figure 12.2
When
the total number of particles N (= Y/mH) coming from the nebula is kept constant, Z(R)
becomes the variable (see equation 12.13). For Y = 1, let us
calculate the residual mass of the star as a function of its
radius R. After temperature stabilization, the relative mass of
the star (with respect to the mass of the initial nebula) as a
function of the radius R is given by equations 12.13 and 12.28.
This is illustrated on figure 12.2.
We see
that when the radius of the nebula (or the star) decreases, the
star loses mass as electromagnetic radiation more and more
rapidly.
12.5 - Maximum Mass of
a Star versus Its Radius.
Let us
assume now that the mass available Y is so large that the
product YZ is always larger than 10. In that case, the value of
the bracket in equation 12.28 reaches a maximum of 1.0. Let us
substitute equation 12.13 in equation 12.28. This gives:
 |
12.29 |
Since
the maximum value of the bracket in equation 12.29 is 1.0, the
maximum value of M{N} as a function of R is:
 |
12.30 |
Equation 12.30 shows that the maximum mass of a star increases
linearly with its radius R. Above this limit, any mass falling
freely on the star reaches a kinetic energy equal to its mass so
that the same amount of radiation energy is freed and there is
no net increase of mass of the star. The incoming particle is
totally transformed into radiation which totally escapes from
the star.
12.6 - Complete
Transformation of Mass into Energy.
There
is another way to find the maximum mass of a star of radius R.
We have seen that the gravitational energy E(Pot) of a particle
of mass m at a distance R from the surface is given by:
 |
12.31 |
We know
that independently of their masses, all particles reach the same
velocity when they fall from outer space to the surface of the
same star. During their fall, particles acquire kinetic energy.
The kinetic component of energy of a particle moving at velocity
v is given by (g-1)m in the equation:
where
 |
12.33 |
During
the fall of a particle in the gravitational potential of a star,
no energy is coming from outside the system. Consequently, the
total energy of the falling particle remains constant during an
unperturbed fall.
This
result is different from the inertial acceleration of a mass
absorbing energy given by an external independent source. Due to
that external source of energy, the total energy of the particle
increases as given by equation 12.32. However, when falling
freely in a gravitational field, the kinetic energy increases at
the expense of the gravitational energy of the particle.
Let us
consider a particle reaching the surface of a star (of maximum
mass). The velocity corresponds to g
= 2 (v = 0.866c). Then the kinetic energy Ek is equal
to the initial mass at rest:
When
the particle hits the surface of the star, the kinetic energy is
released and emitted toward outer space (either immediately as
gamma rays or later as thermal energy). When this happens, the
loss of mass Dm is equal to the mass
of the particle m. At the surface of the star, the kinetic
energy of the particle is equal to the gravitational energy it
has lost. We have:
 |
12.35 |
Therefore, in that limit case, the mass Mlim of the star is:
 |
12.36 |
Consequently, any mass falling from outer space to the distance
Rlim from the star of mass Mlim will be totally annihilated into radiation. As
expected, this result is identical to equation 12.30.
Consequently, when the surface of the star is at such a deep
gravitational potential, there is no possibility of increasing
the mass of the star any further. Finally, if a particle has an
initial velocity toward the star when entering the outer limits
of the gravitational field, more energy will be removed from the
star through radiation than the amount added by the particle.
The mass of the star then decreases since more mass escapes by
radiation than the amount of mass added by the particle.
Of
course, near the surface of a star (which has a maximum mass),
the gravitational potential is enormous so that clocks run at a
very slow rate. Matter located in this extreme gravitational
field will interact according to the proper parameters existing
at that location. Consequently, the spectrum of the Planck
radiation emitted from this deep potential will be emitted
according to the local clock which runs very slowly. The
spectrum will be displaced toward longer wavelengths with
respect to outer space where clocks run more rapidly as
explained in chapter one. However, after its emission from the
location in the deep gravitational potential, light will not be
redshifted again while traveling against the gravitational field
as explained in chapters one and ten.
If we
consider a particle reaching the ultimate potential at a
distance Rlim from the center
of the star, there is no possibility for it to move deeper
inside that radius because there is nothing left of the
particle. It would be absurd to discuss the behavior of
particles at or inside that extreme radius since they no longer
exist and all their energy and mass have been transformed
completely into radiation.
Comparison.
This
relationship for the maximum mass of a star can be compared with
the Schwarzschild radius. Let us note that the Schwarzschild
radius RS has an
incomprehensible meaning in our context. Just as for general
relativity, it is not compatible with the principle of mass-energy
conservation. It is given by the relationship:
 |
12.37 |
12.7 - Proper Values in
Extreme Gravitational Potentials.
Let us
consider that an observer in outer space measures the distances
between the center of a star (having the maximum mass Mlim) and different bodies stationary at different
distances. Using his proper units, the outer space observer can
measure the distances between the center of the star and the
closest body existing around it (which is near Rlim) up to the more distant masses. However, the observers
located on each of those bodies will use their proper units to
make their measurements of their own distance from the center of
the star. They must use these proper values in order to apply
correctly the well-known physical relationships. We have seen that
the absolute length of the meter is longer for an observer located
closer to the star. Consequently, when measuring the same absolute
radius, the number of proper meters will be smaller
for the observer close to the star than for the outer space
observer.
Using
the equations given in chapter four, we see that when the
distance from the star is large (in the Newtonian limit), the number
of proper meters measured by an outer space observer is almost
identical to the number obtained by an observer not too close to
the star. However, when the observer is close to the extreme
minimum radius Rlim, the use of the extremely dilated proper meter will
give a number of proper meters approaching zero
(and not Rlim(o.s.)). For this
reason, physical phenomena taking place near location Rlim (using internal proper values) appear very strange to
an outer space observer.
Near
that location (Rlim), the Bohr
and nuclear radii get very large and the corresponding energy
inside particles becomes extremely small with respect to the
external mechanical forces. In outer space, we are used to see
internal (atomic and nuclear) forces of matter being much larger
that the mechanical and gravitational forces. Near a degenerate
star, nuclear forces are much weaker. This phenomenon favors
reactions between particles.
Let us
also recall that in the first chapters of this book, we were
calculating very small relativistic interactions (i.e. Mercury
precessing around the Sun). It was then enough to consider the
first order of a series expansion. However, when we consider
bodies with kinetic energy in a very deep gravitational
potential, these approximations are no longer accurate.
12.8 - Beyond the
Extreme Gravitational Potential.
Let us
consider a star having a maximum mass and therefore surrounded
by an extreme potential. We have seen that when an hydrogen atom
gets closer to the surface of the star, its mass decreases when
brought to rest and its clock slows down in the same proportion.
We have seen that the same maximum gravitational potential can
exist at the surface of stars having different radii. When the
nucleus of this star approaches that extreme limit of
gravitational potential, the number of particles
forming that star approaches infinity while the mass of each
atom approaches zero. The product of these two parameters
approaches a constant (for a given radius) as shown in equation
12.30.
Finally, extrapolating (to a smaller radius) beyond this extreme
potential, the mass of the falling hydrogen atom disappears at
the same time as the clock becomes infinitely slow and finally
stops running at Rlim. In fact, one can say
indifferently that the clock has stopped running or that the
clock has disappeared and no longer exists. Therefore clocks
become infinitely slow at the same time as they disappear
completely out of existence. In physics, it is absurd to study
matter inside the critical radius Rlim.
12.9 - Formation of
Matter in a Deep Gravitational Potential versus the Formation
of Matter and Anti-Matter.
We have
seen above that mass can be transformed into radiation in a deep
gravitational potential without requiring a reaction between
matter and anti-matter. In physics, there is another well-known
mechanism transforming mass into radiation: the annihilation of
a particle with its anti-particle. For example, we know that an
electron and a positron can be annihilated into radiation. As
expected, the corresponding inverse mechanism is also known from
the interaction of photons creating a pair of matter and
anti-matter. It is important to notice that the reaction of
annihilation of matter with anti-matter is extremely rapid so
that matter formed at the same time (and at the same location)
can survive only during an extremely short time before being
annihilated. Particles and anti-particles destroy each other at
a very high rate. This system is quite unstable. Furthermore,
since matter and anti-matter are formed simultaneously at the
same location, it is ultimately improbable that they could
separate out to form independent galaxies. Consequently, another
mechanism of formation of matter without involving anti-matter
is required to explain our universe if we want to avoid ad hoc
hypotheses.
12.9.1 - Inverse
Gravitational Mechanism.
We have
seen in this chapter how matter falling in a deep gravitational
potential is finally transformed into radiation. This mechanism
cannot be maintained forever in the universe because all matter
would be transformed into radiation. We have explained above how
the formation of matter through the mechanism of matter and
anti-matter cannot lead to the formation of huge clusters of
galaxies of matter in the universe as we observe them. There
must be an equilibrium between the formation and the
annihilation of matter in the universe. Mass-energy conservation
is not compatible with the creationist theory that claims that
the universe was formed from nothing ten or fifteen billion
years ago.
It is
well known in physics that for every mechanism, an inverse
mechanism exists. The simple absorption of radiation by matter
is to some extent an intermediate mechanism of transformation of
energy into mass without involving anti-matter. However, in that
case, atoms become more massive but no new atoms are formed.
A
simplistic description of the inverse mechanism corresponding to
the annihilation of matter in a gravitational field is the
following. Since radiation is emitted when atoms hit a surface
located in a deep gravitational potential, we can foresee that
energetic radiation hitting the surface of the same star could
generate particles with sufficient kinetic energy so that they
could reach the escape velocity vesc ( = 0.866c) of a star with extreme mass and be freed
in outer space. Of course, other mechanisms involving gravity
can be suggested but are beyond the discussion of the present
book.
When
matter falls into an extreme gravitational potential, it is
transformed into energy without involving a reaction between
matter and anti-matter. Consequently, the inverse reaction must
equally correspond to the formation of matter without the
creation of anti-matter. We have seen that a reaction generating
matter plus anti-matter is not acceptable to explain the origin
of matter in the universe, because of the extremely fast inverse
reaction returning matter into radiation. We see now that a
mechanism using gravity can explain the transformation of matter
in the universe.
The
transformation of matter into radiation (and its inverse
reaction) is an extremely slow process since the time for a star
to emit the thermal energy during its formation depends on its
size but generally takes at least a few hundred million years.
One can expect that the inverse reaction transforming radiation
into neutral particles can take a few billion years before
forming nebulae which later evolve into stars and later into
other bodies with a very deep gravitational potential. Such
mechanisms would finally form a complete cycle transforming
matter into radiation and vice versa. On the average this cycle
would repeat itself every ten or fifteen billion years. In such
a case, after a full cycle, the information about the exact
previous structure of the universe would be lost. From this
mechanism, matter of the universe could be recycled
periodically. During that cycle, since there would be large
variations in the time taken by concentrations of masses to
evolve, the universe would always look more or less the same
through time. The possibility of such a mechanism becomes highly
probable when taking into account the red shift mechanism taking
place in our universe as demonstrated [1] in previous papers.
12.10 - References.
[1] P. Marmet, A New
Non-Doppler Redshift, (Book), Physics Dept. Laval
University, Québec, Canada, 64p., 1981.
also:
P. Marmet, A
New Non-Doppler Redshift, Phys. Essays, 1, 24-32,
1988.
also:
P. Marmet, Redshift of Spectral Lines
in the Sun's Chromosphere, IEEE, Transactions on
Plasma Science: Space and Cosmic Plasma 17, 238-243, 1989.
also:
P. Marmet and Grote Reber, Cosmic Matter and the
Non-Expanding Universe, IEEE, Transactions on
Plasma Science, 17, 264-269, 1989.
also:
P. Marmet, Non-Doppler
Redshift of Some Galactic Objects, IEEE,
Transactions on Plasma Science, 18, 1, P. 56-60, 1990.
<><><><><><><><><><><><>
Chapter11 Contents Appendix 1
Return To: List of Papers
on the Web
Where to get a Hard Copy
of this Book
 Einstein's
Theory of Relativity
Einstein's
Theory of Relativity