The Principle of Equivalence.
10.1 - Introduction.
        Among numerous postulates, Einstein proposed the equivalence principle which states that no experiment can distinguish the acceleration due to gravity from the inertial acceleration due to a change of velocity. To illustrate that principle, Einstein used thought experiments involving elevators. He compared different phenomena related to accelerations observed inside an elevator. He purposely limited the range of observations to the frame of the elevator, excluding other predictable consequences that should logically take place inside other frames. The principle of equivalence being a postulate, the reasons for which Einstein did not take into account the motion of his own frame were not explained.
        In physics as in logic, a principle is valid only when it is coherent with all the facts. An exception always disproves the rule. It is surprising to read how the equivalence principle has been generally accepted while it is so easy to prove that it is not coherent with the behavior of bodies located in other frames, as we will see below.

10.2 - Deflection of Light in an Elevator Moving at Constant Velocity.
        Experiments describing a constant relative transverse velocity between a source and an elevator are generally ignored. Let us consider a horizontal parallel beam of light (or particles, as on figure 10.1) projected on an elevator (of negligible mass) moving upward at a constant velocity v with respect to the source. The experiment takes place in outer space far away from any gravitational field.
        Because momentum must be conserved, the beam of light must move in a straight line. On figure 10.1, the dotted line inside the elevator shows where the photons can be detected with respect to the moving elevator at different times. The relative location of the photons with respect to the elevator moving at a constant velocity v is:

10.1
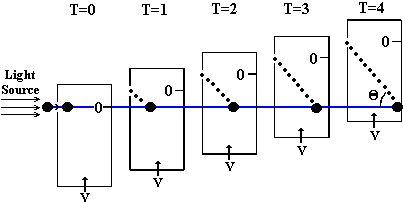
        This problem of constant velocity is simple but rarely considered. Obviously, the beam will not appear to move horizontally for the observer inside the elevator. However, as seen on the external frame, the beam of particles travels horizontally. This shows that the relative transverse velocity between the source and the elevator is measurable.


Figure 10.1

10.3 - Inertial versus Gravitational Acceleration of Masses.
        Before considering the problem of photons moving with respect to an accelerated frame, let us study a mass m moving horizontally. The mass enters an elevator which has an upward acceleration a in outer space at the moment its vertical velocity with respect to the source of the mass is zero. The elevator is accelerated by a rocket placed under it to produce a force F (shown by upward arrows on figure 10.2A). Due to that force F, the elevator (and the observer) accelerates following Newton's law:

F = Ma 10.2
        where M is the mass of the elevator (including the observer's mass) and a is its acceleration given by:
10.3
       After a time interval Dt, the mass will hit the opposite wall. It will have traveled a vertical distance DhA relative to the moving elevator. Obviously, the mass will have traveled an absolute vertical distance of zero since there is no gravitational field.

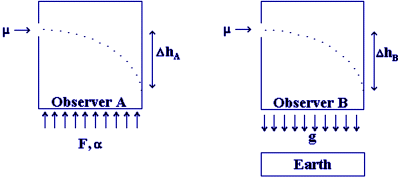
Figure 10.2A                            Figure 10.2B

        Let us consider a similar elevator located at rest on Earth as illustrated on figure 10.2B. The Earth's gravitational field accelerates the mass m toward the Earth's center. After a time interval Dt, when the mass hits the opposite wall of the elevator, it will have traveled an absolute vertical distance DhB.
        In the experiment described on figure 10.2A, the mass m is completely free of any field and any force and therefore cannot gain any absolute energy when the floor of the elevator approaches it. An atomic clock bound to that free mass m will maintain a constant rate since no acceleration (therefore no energy) is given to the electrons or particles of the atomic clock. However, the elevator with the observer will gain kinetic energy (and therefore mass) due to the momentum transferred by the rocket. The observer's clock located on the floor of the elevator will slow down (absolute time) due to its increase of velocity in free space as given in equation 3.9. Consequently, the observer using the moving clock will observe a relative blue shift on light emitted from mass m. Let us note that the Doppler effect is considered separately and has not been taken into account.
        In the experiment described on figure 10.2B, the elevator and the observer cannot gain any energy as a function of time since no work is produced on them. Neither the potential of the observer nor its velocity change. Therefore, the atomic clock of the stationary observer will keep giving a constant rate as a function of time. However, the clock on the falling mass will slow down for two reasons (independent of the Doppler effect): First, because of its increase of velocity (equation 3.10) and second, because of its decrease of potential energy (equation 1.22). Consequently, the observer standing in the elevator will observe a red shift on light emitted by the falling mass m.
        The Doppler contribution to the shift of frequency is identical in figures 10.2A and 10.2B (if a = g). Its amplitude is much more important than the one due to the change of internal mass. However it can be subtracted out to show the difference explained above.
        We see that the principle of mass-energy conservation implies that there is a fundamental difference between an inertial acceleration and an acceleration due to gravity since the consequences of each acceleration are just opposite. In the case of inertial acceleration (figure 10.2A) the clock located on the apparently falling mass will run faster than the observer's clock because of the slowing down of the observer's clock. On the contrary, in the case of gravitational acceleration (figure 10.2B), the falling clock will run more slowly than the observer's clock. One must conclude that the physical properties of the gravitational acceleration are different from the ones of inertial acceleration which means that the gravitational acceleration is not equivalent to the inertial acceleration.

10.4 - Bremsstrahlung Due to Inertial and Gravitational Accelerations.
        To illustrate the difference between inertial and gravitational accelerations, let us consider another thought experiment in which electric charges are placed in a gravitational field. One or more electrons are deposited on a stationary insulator in the Earth's normal gravitational field. This is static electricity. It is well known that Maxwell's equations predict that any accelerated electric charge must emit radiation called bremsstrahlung. According to Einstein's principle of equivalence, charges at rest in the Earth's gravitational field should emit bremsstrahlung because of the gravitational acceleration. However, no experiment has ever detected the emission of bremsstrahlung due to the gravitational acceleration of static electricity. The emission of radiation due to gravitational acceleration has been overlooked.
        There is a way to prove that charges submitted to a gravitational acceleration do not emit bremsstrahlung. The principle of mass-energy conservation requires that energy must be given to an electric charge in order to compensate for the electromagnetic energy emitted during its acceleration. Let us try to identify the origin of the energy responsible for the bremsstrahlung predicted by Maxwell's equations and Einstein's principle of equivalence.
        If bremsstrahlung is emitted when electric charges are submitted to gravity, there must be an energetic mechanism available to compensate for the energy lost by radiation. That continuous emission of radiation due to gravitational acceleration must necessarily extract energy from a source. Therefore, after a long period of time, the accumulated loss of energy in the source will be more easily detectable than the weak bremsstrahlung emitted. In the case of individual electrons stationary in a gravitational field, the only source of energy available is their mass. Consequently, the electron mass should decrease as a function of time to compensate for the electromagnetic energy bound to be emitted. If the electron mass decreases when standing in a gravitational field, one should eventually find electrons with different masses depending on the time they have been submitted to the Earth's gravitational acceleration.
        However, it is observed that electrons maintain their full integrity and do not lose any mass while standing in a gravitational field. All electrons have the same mass. Due to the principle of mass-energy conservation, the absence of any source of energy shows that no bremsstrahlung can be emitted from gravitationally accelerated electrically charged particles. However, in the case of inertial acceleration, the mechanical energy required is well identified and compensates for the electromagnetic energy emitted as bremsstrahlung.
        These considerations show again that gravitational acceleration is different from inertial acceleration. Bremsstrahlung is emitted only when submitted to inertial acceleration. Since Einstein's general relativity is based on Maxwell's equations and the principle of equivalence, we must reexamine Einstein's predictions.

10.5 - Behavior of Light.

10.5.1 - Light Path in an Accelerated Elevator.
        Let us now consider the experiment described in section 10.3 but using light instead of masses (figure 10.3A). Due to the conservation of momentum, light keeps moving in a straight line (as on figure 10.1) and takes a time interval Dt to go across the elevator. Because of the elevator's increasing upward velocity, during the time interval Dt, light seems to travel a vertical distance Dh:

10.4
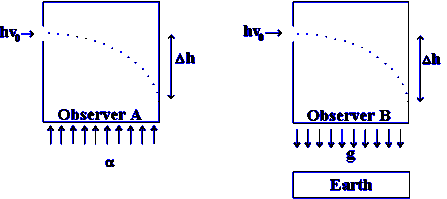
        Therefore, as illustrated on figure 10.3A, for the accelerated observer, the beam of light will appear to follow a curve and will hit the opposite wall at a distance Dh below the entrance height.

        Let us assume that the acceleration due to the rocket produces a change of velocity dv/dt equal to g = 9.8 m/s which is the gravitational acceleration on Earth. Observer A will feel that the upward force of the floor produces the same downward path on the photon as for a massive particle accelerated in the Earth's gravitational field (figures 10.2A and 10.2B).
        However, the accelerated observer A gains velocity and energy due to his increase of velocity. Therefore, his clock will slow down between the time light enters the elevator and the time light reaches the opposite wall of the elevator. Consequently, even if we do not take into account the Doppler blue shift due to the increase of relative velocity of the observer with respect to light, the observer detecting the apparently deflected light will measure an apparent increase of its frequency (blue shift) because of the absolute slowing down of his clock.

10.5.2 - Light Path in a Gravitational Field.
        Let us assume momentarily that the equivalence principle is valid. Therefore, with respect to observer B on figure 10.3B, light entering the room horizontally would be deflected as illustrated. This hypothesis implies that light is attracted by gravity. However, to be valid, we must verify that such an hypothesis is compatible with mass-energy conservation. If light is deflected, let us calculate the energy relationship caused by that deflection.
        Let us call F the hypothetical gravitational force on a photon in the direction of the gravitational acceleration. During its passage across the elevator, we assume that the photon is deflected on a distance Dh in the direction of the force F, as shown on figure 10.3B. Mass-energy conservation requires that a displacement Dh in the same direction of a force F gives an increase of energy DW equal to:

DW = FDh  10.5
        The photon affected by the gravitational force F will then reach the opposite wall with an energy increase of DW at a distance Dh below its initial height. We have seen that the absolute photon energy is proportional to its absolute frequency. Therefore the photon should gain absolute energy and frequency (blue shift) and this should be seen by observer B.
        However we have seen in chapter one that the absolute energy of a photon moving downward does not increase. The Mössbauer experiment shows that there are local changes of clock rate at different altitudes but the absolute energy of the photon does not change. An absolute change of photon energy in a gravitational field is contrary to mass-energy conservation. Consequently:
DW = 0  10.6
        From equation 10.5, since F and Dh have to be in the same direction, the only way to produce a deflection (Dh ¹ 0) with DW = 0 is to have Dh different from zero when F = 0. This means a deflection of photons when there is no force acting on them. This is contrary to Newton's second law on inertia.
        Consequently, to be compatible with mass-energy conservation, there is either no deflection or no force (which leads to no deflection anyway). The curved trajectory on figure 10.3B is erroneous, light must move in a straight line in a gravitational field. We have then:
DW = 0, F = 0 and Dh = 0 10.7
        An observer located straight in front of the entrance aperture on figure 10.3B will observe the beam reaching him at that location without any change of frequency. We conclude that light is apparently deflected with respect to an accelerated observer with an inertial acceleration as illustrated in figure 10.3A. However, as given in equation 10.7, light cannot be deflected by gravity because of mass-energy and momentum conservation. We must conclude again that Einstein's equivalence principle is erroneous which means that the behavior of light is perceived differently by observers subjected to gravitational acceleration and inertial acceleration.
        It has been claimed in the past that such a deflection (by a gravitational field) has been measured experimentally during solar eclipses. The reliability of such results are generally claimed only by those who have never read seriously the original articles describing those experiments. The report given in appendix II gives a shocking proof of the weakness of the experiment. A small deflection of starlight by a gravitational field has been predicted by Einstein. However, it has never been seriously proved experimentally.

10.5.3 - The Equivalence Principle and Light Deflection.
        It has been well recognized that the deflection of light rays is closely related to the equivalence principle discussed above. According to the paper "The Equivalence Principle with Light Rays"[1]:

        Since the equivalence between inertial and gravitational acceleration assumed by Einstein is erroneous as shown above in several independent ways, it is not surprising that its consequence (light deflection) is also erroneous.
        It is well known that Einstein predicted in 1911 that light should be deflected due to the solar gravitational field. In fact, this prediction is almost identical to the one given by Soldner in 1801 using Newton's law. This demonstration can be understood easily. In classical mechanics, the amount of deviation of any massive object passing near the Sun at velocity v is totally independent of the mass of the object. Also, it was assumed that the velocity of light c could be treated as any velocity v. The principle of equivalence implies the equivalence between the inertially accelerated elevator (figure 10.3A) and the gravitationally accelerated photon on figure 10.3B. Due to the force on the elevator and on observer A, the photon hits the opposite wall of the elevator after the elevator has moved up the distance Dh. This apparent deviation, which corresponds to 0.87" near the solar limb (see Figure 10.3A) is clearly the one required in the case of inertial acceleration of the elevator. Assuming the principle of equivalence, the same value should be found in general relativity. However, Einstein's general relativity predicts a deviation of 1.74". That is twice as much as drawn on figure 10.3A).
        The reliability of the apparent deviation illustrated on figure 10.3A is so great that one cannot believe that this amount of deflection could be doubled to satisfy Einstein's predictions of general relativity and the principle of equivalence. Einstein's claim is astonishing. If the opposite wall of that elevator on figure 10.3A is open, that double amount of deflection means that there would be an absolute deflection in a rest frame, even in the absence of any gravitational field. There is no logical way to explain that the amplitude of the deviation in the elevator submitted to inertial acceleration could be twice as much as the one illustrated on figure 10.3A, since the crossing light is subjected to no interaction in a space having zero field and the observer A has certainly moved only through the distance  Dh. One cannot claim that light is deflected just because there exists an observer. If that doubled amount of deviation cannot exist in the case of inertial acceleration, it cannot exist either in a gravitational field without contradicting the equivalence principle on which is based the theory leading to the deviation of light in a gravitational field (1.74").
        Consequently, Einstein's prediction giving a deviation of 1.74" is self contradictory and cannot be compatible with the principle of equivalence.

10.6 - Gravitational Lenses.
        There are several consequences to the fact that light is not deviated in a gravitational field. The deviation of light by a gravitational field gave birth to the claim that rings in space are caused by the focusing of light coming from remote sources by the gravitational mass of intervening galaxies. This explanation is certainly erroneous since light is not deviated by a gravitational field.
        These rings can be explained more logically by the presence of large quantities of ions moving in the magnetic field of a galaxy. It is well known that ions spread naturally into rings in a magnetic field. This is a rational interpretation of a phenomenon that has been erroneously interpreted as Einstein's rings.

10.7 - Attracting Force between Parallel Beams of Charged Particles.
        We have seen in section 10.4 that electrical phenomena can be used to demonstrate that gravitational acceleration is different from inertial acceleration. To end this chapter, we will give an example using electricity disproving the principle of reciprocity (for another proof, see section 3.9).
        In elementary physics, Ampere's law teaches how to calculate the force between two parallel straight conductors carrying currents in the same direction. We learn that a force F between parallel conductors spaced by a distance Dx is induced because the current i' in the second conductor passes in the magnetic field generated by the current i in the first conductor. The force F by unit of length (in MKS units) is:

10.8
        That force is so well recognized in physics that it was used "as the basis of the definition of the ampere in the MKS system" [2]. The force between these conductors is attractive when the currents are in the same direction and repulsive when the currents are in opposite directions.
        With the modern development of accelerators and intense beams of charged particles, the electric conductor is no longer necessary to observe this phenomenon and the interaction of independent electric charges in the magnetic field generated by comoving electric charges has been observed directly. In fact, the magnetic field produced by comoving electric charges produces a focusing that reduces the dispersion of the beam of particles. One can clearly observe particles all having the same velocity in a parallel beam attracting each other due to the magnetic field produced by the velocity of the neighboring charges.
        Let us now consider an observer moving with that beam of particles. In his frame of reference, the particles appear stationary with respect to him. Then, no magnetic field is produced. Using Einstein's principle of reciprocity within that moving frame, the charged particles should repel each other according to the electrostatic repulsion of charges having the same polarity. However, they attract each other as calculated above and observed experimentally. This is clearly not acceptable. Other experiments involving Maxwell's equations exist which are not compatible with the reciprocity principle. However, the ones described above suffice to disprove this principle.

10.8 - References.

[1] http://altair.syr.edu:2024/lightcone/equivalence.html
[2] F. W. Sears, Principles of Physics, Addison-Wesley, p. 267, 1946

<><><><><><><><><><><><>

Chapter9   Contents    Chapter 11

Return To: List of Papers on the Web
Where to get a Hard Copy of this Book
Author address